Étude des systèmes électriques : Condensateur et circuit RC
Étude des systèmes électriques/Condensateur et circuit RC
Une page de Wikiversité.
| Chapitre 1 | |||
| Leçon : Étude des systèmes électriques | |||
|---|---|---|---|
| Retour au | sommaire | ||
| Chap. suiv. : | Bobine d'induction et circuit RL | ||
Sommaire[masquer] |
[modifier] Le condensateur
Il existe différentes formes et différents types de condensateurs. Un condensateur est un dipôle constitué de 2 lames métalliques (les armatures) séparées par un isolant (aussi appelé diélectrique).
Rôle du condensateur : il permet d'emmagasiner l'énergie et de la redistribuer quand il y en a besoin.
[modifier] Charge d'un condensateur
Lorsqu'on soumet le condensateur à une tension électrique, il se charge. Une fois chargé, il conserve ses charges sur ses armatures même lorsqu'on le débranche : c'est un réservoir électrique. Si on relie les deux bornes d'un condensateur chargé par un fil électrique il se décharge immédiatement ; il ne faut donc pas toucher les deux bornes d'un condensateur chargé (il y a un risque de choc électrique).
[modifier] Description du fonctionnement
Le générateur peut être considéré comme une pompe à électrons. À chaque fois qu'un électron arrive sur l'armature a un électron de l'armature b se dirige vers la borne positive de la pile. Si une charge négative quitte l'armature b alors il apparait sur cette armature une charge positive. À chaque instant qa = − qb. Petit à petit, il se crée une différence de potentiel électrique entre les armatures a et b. Quand cette différence de potentiel (c'est-à-dire la tension) est égale à celle de la pile, le condensateur est chargé. Le courant ne circule plus dans le circuit.
[modifier] Relation entre intensité et charge du condensateur
[modifier] Définition de l'intensité
La variation d'intensité dans un condensateur est décrite par la formule suivante :
|
donc |
|
|
où q est la charge électrique portée par l'une des deux armatures et exprimée en coulomb (symbole C). Cette intensité peut être soit positive soit négative, selon que le condensateur se charge ou se décharge.
[modifier] Relations entre les charges
Un électron a une charge négative. Lorsqu'un condensateur est chargé, l'une des armatures présente un excès d'électrons et l'autre armature présente un défaut d'électrons. Soit un condensateur constitué de deux armatures notées a et b. Les charges aux bornes d'un condensateur sont égales mais opposées. On note :
 |
[modifier] Capacité d'un condensateur
La charge q d'un condensateur est proportionnelle à la tension à ses bornes. On note :
|
|
C est la capacité du condensateur, elle s'exprime en farads (symbole F).
Comme le farad est une unité très grande, les capacités que l'on rencontre le plus fréquemment s'échelonnent entre 10 − 3 et 10 − 12 farad, c'est-à-dire entre le millifarad (mF) et le picofarad (pF).
[modifier] Condensateur en convention récepteur
Lors de la charge ou de la décharge du condensateur, q change.
q est une fonction du temps : q(t).
 or q(t) = C.uC(t) donc
or q(t) = C.uC(t) donc 
 pour u et i de sens « opposés ». Si u et i sont de même « sens » :
pour u et i de sens « opposés ». Si u et i sont de même « sens » : 
[modifier] Réponse d'un circuit RC à un échelon de tension
On appelle échelon de tension le passage brutal de la tension d'une valeur nulle à une valeur non nulle.

[modifier] Équation différentielle
D'après la loi d'additivité des tensions, 
D'après la loi d'Ohm, 
Donc 
Par définition 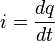 et
et 
Donc 
Donc 
Équation différentielle du circuit RC :
 |
[modifier] Solution
La solution de cette équation différentielle est de la forme 
- quand
 d'où
d'où 
- quand
 ,
,  d'où
d'où 




- Or cela est valable pour toute valeur de t, et notamment pour t = 0 donc
 donc
donc 
- Solution de l'équation différentielle :
Tension aux bornes du condensateur en fonction du temps lors de la charge :

 . . |
[modifier] Constante de temps du circuit RC
[modifier] Expression et analyse dimensionnelle
On pose 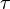 (tau) tel que
(tau) tel que  Cherchons la dimension de
Cherchons la dimension de 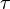 :
:
![R = frac{u}{i} = frac{[V]}{[A]}](http://upload.wikimedia.org/math/5/5/b/55bb15c956478c43d47316a263013ce4.png) et
et ![C = frac{q}{u} = frac{i.t}{u} = frac{[A].[s]}{[V]}](http://upload.wikimedia.org/math/3/c/0/3c09d597f66f5b0c50653ed74f356a28.png)
or  donc
donc ![tau, = frac{[V].[A].[s]}{[A].[V]}](http://upload.wikimedia.org/math/c/2/8/c2819b999cfa07846392c5e3d51d0d29.png)
 |
|
Le produit R.C est donc un temps. En unités internationales, 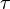 s'exprime en secondes. On l'appelle la constante de temps du circuit RC.
s'exprime en secondes. On l'appelle la constante de temps du circuit RC.
[modifier] Détermination de la constante de temps
- Tracer la courbe de la tension aux bornes du condensateur en fonction du temps lors de sa charge.
- Tracer une droite d'ordonnée la valeur finale de la charge (umax) du condensateur.
- Tracer une droite, partant de l'origine de la courbe et tangente à la courbe en ce même point.
- Le point d'intersection des ces deux droites à lieu à l'abscisse d'instant τ et à cette abscisse, l'ordonnée de la courbe vaut

Au cours de la charge du condensateur à travers une résistance R, sous une tension E du générateur :
- À t = τ, uC = 0,63E
- À t = 5τ, uC = 0,99E (Le condensateur est pratiquement chargé)
[modifier] Influence des caractéristiques du circuit RC sur τ
Comme on l'a vu plus haut,  , Cela implique que,
, Cela implique que,
- Si R augmente, τ augmente;
- Si C augmente, τ augmente.
[modifier] Décharge d'un condensateur dans une résistance

[modifier] Établissement de l'équation différentielle
D'après la loi d'additivité des tensions, 
Or  et
et 
On remplace : 
Soit
 |
[modifier] Solution
On a une solution de la forme 
- On injecte dans l'équation différentielle :



- Par identification des coefficients,

- d'où
 , de même on trouve
, de même on trouve 
- Les conditions initiales donnent A :
à  d'où
d'où 
- Solution de l'équation différentielle :

soit
 |
[modifier] Énergie dans un condensateur
En convention récepteur, la puissance du condensateur s'écrit: p(t)=u(t)*i(t) Or, i(t)=C(du/dt)
On a donc p(t)=u(t)*C(du/dt)=0.5*C*(du²/dt)
Puis dE/dt=p(t), on en déduit:
E(t)=0.5*C*u²;
L'expression de l'énergie dans un condensateur dépend du temps. Sa formule est la suivante :
 |
Démonstration :
L'énergie électrique fournie et emagasinée lors de la charge sous une tension u est de la forme :
 |
En effet,
| P = u.i = u.C.du / dt = 1 / 2C.du2 / dt |
[modifier] Valeur Équivalente
Il est possible de calculer la valeur équivalentes de plusieurs condensateurs:
- En série:

- En parallèles : C1 + C2... + Cn = Ceq
Étude des systèmes électriques : Bobine d'induction et circuit RL
Étude des systèmes électriques/Bobine d'induction et circuit RL
Une page de Wikiversité.
Cette page n'est pas finie. Elle est en phase d'écriture ou de restructuration importante.
|
| Chapitre 2 | |||
| Leçon : Étude des systèmes électriques | |||
|---|---|---|---|
| Chap. préc. : | Condensateur et circuit RC | ||
| Chap. suiv. : | Oscillations libres dans un circuit RLC | ||
Sommaire[masquer] |
[modifier] La bobine
Dans le cas général, une bobine est un dipôle formé par l'enroulement d'un long fil de cuivre autour d'un noyau métallique.
Rôle de la bobine : Elle permet de ralentir l'établissement et la rupture du courant dans un circuit électrique.
[modifier] Action de la bobine
schéma d'un circuit RL
Lorsqu'on soumet une bobine à un courant d'une intensité I, on observe que l'intensité du circuit augmente progressivement jusqu'à atteindre l'intensité I fournie par le générateur. À présent si l'on coupe l'alimentation de ce circuit, l'intensité le parcourant n'atteint 0 qu'au bout d'un laps de temps, la bobine permet donc de ralentir l'installation ou la disparition de l'intensité dans un circuit.
[modifier] Description du fonctionnement
[modifier] Équation différentielle
Grâce à la loi d'additivité des tensions, on peut écrire : E = uL + uR
Rappelons également que d'après la loi d'Ohm, nous avons:Ur = R.i
On a alors  avec r la résistance interne de la bobine. D'où :
avec r la résistance interne de la bobine. D'où :
 |
Étude des systèmes électriques : Oscillations libres dans un circuit RLC
Étude des systèmes électriques/Oscillations libres dans un circuit RLC
Une page de Wikiversité.
| Chapitre 3 | |||
| Leçon : Étude des systèmes électriques | |||
|---|---|---|---|
| Chap. préc. : | Bobine d'induction et circuit RL | ||
Sommaire[masquer] |
[modifier] Étude expérimentale
[modifier] Circuit d'étude
[modifier] Observations
- Interrupteur en position 1 : charge du condensateur
- Interrupteur en position 2 : décharge
On observe des oscillations électriques amorties pseudo-périodiques. On note  la pseudo-période des oscillations.
la pseudo-période des oscillations.
[modifier] Influence de R
Si, en partant d'un régime pseudo-périodique, on augmente progressivement R, les oscillations s'amortissent de plus en plus vite. On observe également une augmentation de la pseudo-période. Lorsque la résistance atteint une valeur critique, il n'y a plus d'oscillations. Au dela de cette valeur critique, aucun comportement oscillant n'est observé
[modifier] Influence de L et C
- Si on garde la même valeur de la capacité et qu'on augmente l'inductance de la bobine,
 augmente.
augmente. - Si on garde la même valeur d'inductance et qu'on augmente la capacité du condensateur,
 augmente également.
augmente également.
[modifier] Étude analytique d'un circuit oscillant
On note :
 la capacité du condensateur
la capacité du condensateur la résistance du conducteur ohmique
la résistance du conducteur ohmique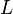 l'inductance de la bobine
l'inductance de la bobine sa résistance interne
sa résistance interne
[modifier] Équation différentielle
D'après la loi d'additivité des tensions,


- or

Donc 
Où  est la dérivée seconde de la tension aux bornes du condensateur en fonction du temps. On la note aussi
est la dérivée seconde de la tension aux bornes du condensateur en fonction du temps. On la note aussi  , par extension de la notation
, par extension de la notation  .
.
Dans la suite, on étudie un cas particulier de circuit, sans résistance. Le terme dissipatif est donc négligé afin de simplifier la résolution de cette équation différentielle.
[modifier] Cas du circuit LC
Un circuit LC est un circuit RLC sans résistance. Ce circuit est dit idéal, puisqu'il ne peut être réalisé.
L'équation différentielle se réduit donc à :

[modifier] Solutions
La fonction mathématique dont la dérivée seconde est l'opposée d'elle-même à une constante près est la fonction cosinus.
Les solutions sont donc de la forme  , avec :
, avec :
 : amplitude (tension maximale, en Volts)
: amplitude (tension maximale, en Volts)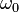 : pulsation (rad.s⁻¹)
: pulsation (rad.s⁻¹) : phase à l'origine
: phase à l'origine
On appelle  la phase.
la phase.
On a  et
et  .
.
 et
et  ne dépendent que des conditions initiales,
ne dépendent que des conditions initiales, 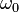 dépend des grandeurs électriques du circuit.
dépend des grandeurs électriques du circuit.
[modifier] Détermination de la pulsation
On a  .
.
Or 
Donc 
D'où 
On a donc :
 |
[modifier] Détermination des autres constantes (A et phi)
 va dépendre de la façon dont on a chargé le condensateur
va dépendre de la façon dont on a chargé le condensateur va dépendre du choix de l'instant initial
va dépendre du choix de l'instant initial
On prend comme instant initial l'instant  où
où  et
et  .
.
Donc  , or
, or 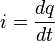
D'où 
 .
.
Or comme  , d'après
, d'après  ,
, 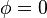 et
et  .
.
En prenant ces conditions initiales, l'expression de la tension aux bornes du condensateur est donc :
 |
[modifier] Relation entre la pulsation et la pseudo période
On utilise  . On sait qu'une fonction cosinus reprend la même valeur quand l'angle a augmenté de
. On sait qu'une fonction cosinus reprend la même valeur quand l'angle a augmenté de  et aussi au bout d'une période.
et aussi au bout d'une période.
Donc 

 d'où
d'où  .
.
 : période propre des oscillations libres d'un circuit LC
: période propre des oscillations libres d'un circuit LC
[modifier] Influence de la résistance du circuit
- Si
 , le régime est périodique de période
, le régime est périodique de période 
- Si la résistance est faible, le régime est pseudo périodique de période

- Si la résistance est importante, le régime est dit apériodique
[modifier] Interprétation énergétique
[modifier] Régime périodique (LC)

L'énergie passe sans perte du condensateur vers la bobine.
Exemples :
[modifier] Régime pseudo-périodique
 et
et  décroît.
décroît.
L'énergie est perdue par effet Joule dans les résistances (conducteur ohmique et résistance interne de la bobine).
[modifier] Entretien des oscillations
Un moyen pour entretenir les oscillations est de compenser la perte d'énergie par un apport extérieur (bien ajusté : au même rythme que les oscillations).
Il existe un circuit, appelé Amplificateur opérationnel (ou ampli-op, AO…) qui est capable de donner de l'énergie à un circuit RLC. Monté convenablement, il peut se comporter comme une résistance négative.
La partie encadrée en rouge du premier circuit permet de simuler une résistance négative. La tension aux bornes de ce système est alors  . L'équation différentielle du circuit est donc
. L'équation différentielle du circuit est donc 
Si on ne veut pas d'amortissement des oscillations, on doit avoir  , ce qui revient à
, ce qui revient à  , c'est-à-dire régler
, c'est-à-dire régler  à la même valeur que la somme des résistances présentes dans le circuit.
à la même valeur que la somme des résistances présentes dans le circuit.
Si on règle différemment  on peut avoir :
on peut avoir :
- des oscillations toujours amorties si
 n'est pas assez grande (en valeur absolue), c'est-à-dire si
n'est pas assez grande (en valeur absolue), c'est-à-dire si  est trop petite
est trop petite - des oscillations non sinusoïdales si
 est trop importante (en valeur absolue), c'est-à-dire si
est trop importante (en valeur absolue), c'est-à-dire si  est trop grande
est trop grande
En pratique,  doit être légèrement supérieure à la somme des résistances du circuit à cause de la résistance des fils conducteurs.
doit être légèrement supérieure à la somme des résistances du circuit à cause de la résistance des fils conducteurs.




![[A] = frac{[C]}{[s]}](http://upload.wikimedia.org/math/4/f/a/4fa71eb30516bc02fe9d9cdc37016cbf.png)


![[C] = [F]times [V]](http://upload.wikimedia.org/math/1/6/c/16ce296c08c94e501dbf4d61c8d3c85e.png)

![tau = [s],](http://upload.wikimedia.org/math/f/b/d/fbd4856d7b7b264887dce0d9374a8025.png)










