Étude de fonctions : Limites et asymptotes
Étude de fonctions/Limites et asymptotes
Une page de Wikiversité.
| Chapitre 1 | |||
| Leçon : Étude de fonctions | |||
|---|---|---|---|
| Retour au | sommaire | ||
| Chap. suiv. : | Taux de variation | ||
Sommaire[masquer] |
[modifier] Approche
- Soit
 .
.
Que se passe-t-il lorsque x devient de plus en plus grand, autrement dit, lorsque x tend vers l'infini ?
f(x) tend également vers l'infini.
On note :  .
.
On énonce : « la limite de f(x) quand x tend vers  est égale à
est égale à  ».
».
De même, nous pouvons écrire : 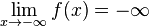 .
.
Intéressons-nous maintenant à une valeur précise de x. Par exemple, pour x = 4, f(x) = 8. Mais alors si x tend vers 4, f(x) va s'approcher de plus en plus de f(4) = 8 :  .
.
- Soit
 .
.
Si a est un réel quelconque, on a bien :  .
.
Lorsque x devient très grand, nous pouvons concevoir que  devient très petit, se rapprochant de 0 :
devient très petit, se rapprochant de 0 :  .
.
De même, quand x prend des valeurs négatives très petites,  .
.
- Soit
 . Essayons de calculer sa limite aux infinis :
. Essayons de calculer sa limite aux infinis :
|
|
or nous savons que :
|
|
donc |
|
| Plus généralement, calculons la limite d'une fonction polynôme :
Soit
|
Or, lorsque 0 < j < n :
|
Nous retiendrons qu'une fonction polynôme se comporte, aux infinis, comme son terme de plus haut degré.
[modifier] Définition
[modifier] Limite finie en l'infini
- Soit f une fonction définie d'un nombre réel jusqu'à l'infini. Soit l un nombre réel. On dit que f tend vers l quand x tend vers
 si et seulement si tout intervalle ouvert contenant l contient aussi toutes les valeurs de f(x) pour x assez grand. On écrit :
si et seulement si tout intervalle ouvert contenant l contient aussi toutes les valeurs de f(x) pour x assez grand. On écrit :

- On dit que f tend vers l quand x tend vers
 si et seulement si tout intervalle ouvert contenant l contient aussi toutes les valeurs de f(x) pour − x assez grand (ou x assez petit, x pouvant être négatif). On écrit :
si et seulement si tout intervalle ouvert contenant l contient aussi toutes les valeurs de f(x) pour − x assez grand (ou x assez petit, x pouvant être négatif). On écrit :

[modifier] Interprétation graphique
Cf admet une asymptote horizontale d'équation y = l au voisinage de 
L'asymptote d'une courbe représentative d'une fonction dans un plan est une droite qui partage une limite commune avec la fonction étudiée. L'équation de cette asymptote dépend de la situation de la limite commune (en l'infini ou en un point...)
[modifier] Limite infinie en l'infini
- On dit que la fonction f tend vers
 quand x tend vers
quand x tend vers  si et seulement si tout intervalle
si et seulement si tout intervalle ![]lambda ; +infty[](http://upload.wikimedia.org/math/8/b/5/8b55cb17bec2ad56524cebeecc8b321a.png) avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment grand. On écrit :
avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment grand. On écrit :
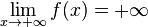
- On dit que la fonction f tend vers
 quand x tend vers
quand x tend vers  si et seulement si tout intervalle
si et seulement si tout intervalle ![]-infty ; lambda[](http://upload.wikimedia.org/math/0/2/6/026b23c74043bfdfb93a95da70fd0a6d.png) avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment grand. On écrit :
avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment grand. On écrit :
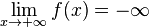
- On écrit :
 ou
ou 
si et seulement si tout intervalle ![]lambda ; +infty[](http://upload.wikimedia.org/math/8/b/5/8b55cb17bec2ad56524cebeecc8b321a.png) avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment petit.
avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment petit.
- On écrit :
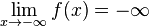 ou
ou 
si et seulement si tout intervalle ![]-infty ; lambda[](http://upload.wikimedia.org/math/0/2/6/026b23c74043bfdfb93a95da70fd0a6d.png) avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment petit.
avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment petit.
[modifier] Limite finie ou infinie en un nombre
- Soit f une fonction définie sur un intervalle ouvert I contenant un nombre réel a.
On dit que f tend vers l quand x tend vers a si et seulement si tout intervalle ouvert contenant l contient aussi toutes les valeurs de f(x) pour tout réel x de I assez proche de a. On écrit :


- On dit que f tend vers
 quand x tend vers a si et seulement si tout intervalle
quand x tend vers a si et seulement si tout intervalle ![]lambda ; +infty[](http://upload.wikimedia.org/math/8/b/5/8b55cb17bec2ad56524cebeecc8b321a.png) avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment proche de a. On écrit :
avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment proche de a. On écrit :

- On dit que f tend vers
 quand x tend vers a si et seulement si tout intervalle
quand x tend vers a si et seulement si tout intervalle ![]-infty ; lambda [](http://upload.wikimedia.org/math/0/2/6/026b23c74043bfdfb93a95da70fd0a6d.png) avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment proche de a. On écrit :
avec λ un nombre réel contient toutes les valeurs de f(x) pour x suffisamment proche de a. On écrit :
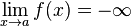
[modifier] Interprétation graphique
Si  (ou
(ou  ) alors Cf admet une asymptote verticale d'équation x = a au voisinage de
) alors Cf admet une asymptote verticale d'équation x = a au voisinage de  .
.
[modifier] Limite aux infinis de fonctions de référence
[modifier] Exemple 1
| Si a > 0 | Si a < 0 |
 |
 |
 |
 |
[modifier] Exemple 2

[modifier] Exemple 3


[modifier] Exemple 4
avec 

[modifier] Exemple 5

[modifier] D'autres outils pour les limites
[modifier] Théorèmes
[modifier] Théorème de comparaison
Soit f et g deux fonctions définies sur un intervalle du type ![]lambda ; +infty[](http://upload.wikimedia.org/math/8/b/5/8b55cb17bec2ad56524cebeecc8b321a.png) (ou
(ou ![]-infty ; lambda[](http://upload.wikimedia.org/math/0/2/6/026b23c74043bfdfb93a95da70fd0a6d.png) ) avec λ un nombre réel telles que pour tout x appartenant à cette intervalle,
) avec λ un nombre réel telles que pour tout x appartenant à cette intervalle, 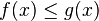 .
.
Si  alors
alors 
[modifier] Théorème des gendarmes
Soit f, g et h trois fonctions définies sur un intervalle du type ![]lambda ; +infty[](http://upload.wikimedia.org/math/8/b/5/8b55cb17bec2ad56524cebeecc8b321a.png) (ou
(ou ![]-infty ; lambda[](http://upload.wikimedia.org/math/0/2/6/026b23c74043bfdfb93a95da70fd0a6d.png) ) avec λ un nombre réel telles que pour tout x appartenant à cette intervalle,
) avec λ un nombre réel telles que pour tout x appartenant à cette intervalle,  .
.
Si  avec a un nombre réel ou
avec a un nombre réel ou  ou
ou  alors
alors 
[modifier] Asymptotes
Regardons la courbe représentative de la fonction inverse.
Cette courbe, lorsque x est de plus en plus grand ou de plus en plus petit, se rapproche de l'axe des abscisses mais sans la toucher. Cette dernière est en fait une asymptote horizontale de la fonction inverse.
De même, la courbe se rapproche également de l'axe des ordonnées, sans jamais la croiser, lorsque x tend vers 0. Nous avons là une asymptote verticale de la fonction.
[modifier] Asymptote horizontale et verticale
Dire que la courbe représentative d'une fonction f se rapproche d'une droite horizontale d'équation y = a quand x devient très grand (ou très petit) signifie que f(x) tend vers la valeur a quand x tend vers l'infini.
Ainsi, la droite  est asymptote horizontale de f si et seulement si
est asymptote horizontale de f si et seulement si  .
.
Quand la courbe représentative de f rapproche d'une droite verticale d'équation  , c'est f(x) qui tend vers l'infini cette fois, lorsque x se rapproche de cette valeur b.
, c'est f(x) qui tend vers l'infini cette fois, lorsque x se rapproche de cette valeur b.
On a : 
Chercher une asymptote horizontale d'une fonction revient à calculer la limite en  de cette fonction.
de cette fonction.
Lorsqu'il y a une asyptote verticale en x = b, la courbe de la fonction ne touche pas la droite, et donc f(b) n'est pas définie ; il s'agit d'une borne du domaine de définition de la fonction.
Chercher une asymptote verticale d'une fonction revient alors à calculer les limites aux bornes du domaine de définition de cette fonction.
[modifier] Asymptote oblique
Soit fune fonction définie sur un intervalle ![I = ]lambda ; +infty[](http://upload.wikimedia.org/math/0/f/a/0fadda389d023efe94996b6c0656e80c.png) (ou
(ou ![]-infty ; lambda[](http://upload.wikimedia.org/math/0/2/6/026b23c74043bfdfb93a95da70fd0a6d.png) ) avec λ un nombre réel telle que l'on ait :
) avec λ un nombre réel telle que l'on ait :
![lim_{+infty (-infty)}[f(x) - (ax + b)] = 0](http://upload.wikimedia.org/math/6/e/5/6e5d98be44cbbac12528b343560f6f46.png)
Alors la droite d'équation y = ax + b est une asymptote oblique à la courbe représentative de f au voisinage de  (ou
(ou  )
)
[modifier] Limite de la composée de deux fonctions
Les lettre a, b et c désignent soit des nombres réels, soit  soit
soit  .
.
Soit la fonction composée  définie sur un intervalle I contenant a, ou dont a est une borne.
définie sur un intervalle I contenant a, ou dont a est une borne.
Si  et si
et si  alors
alors 
Étude de fonctions : Taux de variation
Étude de fonctions/Taux de variation
Une page de Wikiversité.
| Chapitre 2 | |||
| Leçon : Étude de fonctions | |||
|---|---|---|---|
| Chap. préc. : | Limites et asymptotes | ||
| Chap. suiv. : | Continuité | ||
Si f est définie en a et en a + h alors le taux de variation t de f entre a et a + h est :  (avec h ≠ 0)
(avec h ≠ 0)
La limite du taux de variation est égal au nombre dérivé de f en a.

Étude de fonctions : Continuité
Étude de fonctions/Continuité
Une page de Wikiversité.
| Chapitre 3 | |||
| Leçon : Étude de fonctions | |||
|---|---|---|---|
| Chap. préc. : | Taux de variation | ||
| Chap. suiv. : | Nombre dérivé de fonctions | ||
Sommaire[masquer] |
[modifier] Définition
Si une fonction f est continue en a alors f est définie en a et admet une limite finie en a qui est f(a).
Soit f une fonction définie sur un intervalle I et a un nombre de I. On dit que f est continue en a si et seulement si :
 ou
ou  .
.
Sinon, f est discontinue en a.
f est continue sur l'intervalle I si et seulement si, f est continue en tout nombre de I.
[modifier] Interprétation graphique
f est continue sur l'intervalle I signifie que l'on peut tracer la courbe de la fonction f sur I sans avoir à lever le crayon de la feuille.
[modifier] Fonctions classiques
Toutes les fonctions 
 sont définies et continues sur
sont définies et continues sur  . Par conséquent, toutes les fonctions polynômes sont définies et continues sur
. Par conséquent, toutes les fonctions polynômes sont définies et continues sur  . Les fonctions rationnelles sont continues sur tout intervalle où elles sont définies. La fonction sinus et la fonction cosinus sont continues sur
. Les fonctions rationnelles sont continues sur tout intervalle où elles sont définies. La fonction sinus et la fonction cosinus sont continues sur  . La fonction racine carrée est continue sur
. La fonction racine carrée est continue sur  .
.
[modifier] Opérations sur les fonctions continues
[modifier] Opérations classiques
[modifier] Théorème
Soit f et g deux fonctions définies sur un intervalle I, soit a un élément de I où f et g sont continues. Alors leur somme f + g , leur produit  et leur quotient
et leur quotient  (si g(a) ≠ 0) et toutes fonctions du type kf , (
(si g(a) ≠ 0) et toutes fonctions du type kf , ( ) sont des fonctions continues en a. Ceci est démontrable par les propriétés sur les limites.
) sont des fonctions continues en a. Ceci est démontrable par les propriétés sur les limites.
[modifier] Corollaire
Soit f et g deux fonctions définies et continues sur un intervalle I. Alors leur somme f + g , leur produit  et leur quotient
et leur quotient  (si g(x) ≠ 0
(si g(x) ≠ 0  ) et toutes fonctions du type kf , (
) et toutes fonctions du type kf , ( ) sont des fonctions continues sur l'intervalle I.
) sont des fonctions continues sur l'intervalle I.
[modifier] Continuité et composition
[modifier] Théorème
Soit f une fonction définie dans un intervalle I contenant le nombre a et g une fonction définie sur un intervalle J contenant f(a). Si f est continue en a et si g est continue en f(a) alors,  est continue en a.
est continue en a.
[modifier] Corollaire
Si f est définie et continue sur un intervalle I et si g est définie et continue sur un intervalle J contenant f(I). Alors,  est définie et continue sur I.
est définie et continue sur I.
[modifier] Conclusion (théorème)
Si  et si g est continue en l alors,
et si g est continue en l alors,  .
.
[modifier] Résolution de l'équation f(x) = k
[modifier] Théorème des valeurs intermédiaires
Si f est une fonction définie et continue sur un intervalle I et si a et b sont deux nombres de I alors, pour tout nombre k compris entre f(a) et f(b) il existe au moins un réel c compris entre a et b tel que f(c) = k.
[modifier] Corollaire
Si f est une fonction définie, continue et monotone sur l'intervalle [a;b], a < b. Alors, pour tout nombre k compris entre f(a) et f(b) il n'existe qu'un seul nombre c compris entre a et b tel que f(c) = k.
L'équation f(x) = k a une et une seule solution dans [a;b].
[modifier] Cas général
Si f est une fonction définie, continue et strictement monotone sur un intervalle I et si α et β sont les limites de f aux bornes de cet intervalle (α et β sont des nombres,  ou
ou  ). Alors, pour tout réel k strictement compris entre α et β, il existe une et une seule solution à l'équation f(x) = k.
). Alors, pour tout réel k strictement compris entre α et β, il existe une et une seule solution à l'équation f(x) = k.
Étude de fonctions : Nombre dérivé de fonctions
Étude de fonctions/Nombre dérivé de fonctions
Une page de Wikiversité.
| Chapitre 4 | |||
| Leçon : Étude de fonctions | |||
|---|---|---|---|
| Chap. préc. : | Continuité | ||
| Chap. suiv. : | Dérivation | ||
Soit t le taux de variation de f entre a et a + h
Sommaire[masquer] |
[modifier] Condition de dérivabilité d'une fonction en un point
Soit f une fonction définie sur un intervalle I et soit a un nombre de I. On dit que la fonction f est dérivable en a si et seulement si Il existe un nombre réel m tel que l'une des deux propositions suivantes soit vérifiée :
- :

- Pour tout réel h tel que
 on a :
on a :

où φ est une fonction telle que 
[modifier] Les deux propositions sont équivalentes (démonstration)
On suppose que 


On pose  .
. 


 avec
avec 
[modifier] Nombre dérivé
Le nombre réel m est appelé nombre dérivé de f en a. Ce nombre dérivé est noté  .
.
[modifier] À retenir
- Si f est dérivable en a alors le nombre dérivé en a est égal à la limite du taux de variation en a.

- Théorème : Si f est une fonction dérivable en a alors f est continue en a :
"f est dérivable en a" 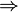
 (avec
(avec  )
)
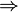

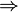

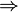

or 
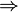

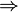 "f est continue en a"
"f est continue en a"
[modifier] Tangente à la courbe d'une fonction en un point (équation cartésienne)
Soit f une fonction dérivable en a et soit C sa représentation graphique. La tangente à la courbe C au point A(a;f(a)) admet pour équation  .
.
Si  alors la droite d'équation x = a est une tangente verticale au point A(a;f(a)) à C mais f n'est pas dérivable en a.
alors la droite d'équation x = a est une tangente verticale au point A(a;f(a)) à C mais f n'est pas dérivable en a.
[modifier] Démonstration
 est le coefficient directeur de la tangente donc une équation cette droite est :
est le coefficient directeur de la tangente donc une équation cette droite est :  . A(a;f(a)) appartient à la tangente donc ses coordonnées vérifient :
. A(a;f(a)) appartient à la tangente donc ses coordonnées vérifient :



donc une équation de la tangente est :


Étude de fonctions : Dérivation
Étude de fonctions/Dérivation
Une page de Wikiversité.
| Chapitre 5 | |||
| Leçon : Étude de fonctions | |||
|---|---|---|---|
| Chap. préc. : | Nombre dérivé de fonctions | ||
| Chap. suiv. : | Fonction dérivée | ||
Sommaire[masquer] |
[modifier] Définition
- Dérivée
- Soit une fonction f, à valeurs dans
 , définie sur un voisinage de x0. On note Δx = x − xo la variation autour du point xo et Δf = f(x) − f(xo) la variation correspondante de la fonction f.
, définie sur un voisinage de x0. On note Δx = x − xo la variation autour du point xo et Δf = f(x) − f(xo) la variation correspondante de la fonction f.
|
Définition no 1 |
|
On dit qu'une fonction f est dérivable en x0 si la limite  existe. Dans ce cas, on appelle cette limite dérivée de f en x0 et on la note |
|
Définition no 2 |
|
On dit que f est dérivable sur un intervalle I si elle est dérivable en tout point de I et on note La dérivée de et par récurrence, on définit la dérivée nième de f, notée f(n). |
Attention à ne pas confondre avec la puissance nième de f, notée fn, avec la dérivée nième notée f(n).
La définition suivante est souvent utile:
|
Définition no 3 |
On dit que f est n fois dérivable sur un intervalle I si elle est n fois dérivable en tout point de I; on dit que si si  Donc |
[modifier] Interprétation
[modifier] Interprétation géométrique
- Si f est à valeurs réelles et si le nombre
 existe, il est est égal à la pente de la tangente à f(x) au point x0. L'équation cartésienne de la droite tangente à f(x) en x0 s'écrit
existe, il est est égal à la pente de la tangente à f(x) au point x0. L'équation cartésienne de la droite tangente à f(x) en x0 s'écrit  . À noter que si
. À noter que si  la tangente à la courbe existe encore, mais elle est verticale, et d'équation x = x0.
la tangente à la courbe existe encore, mais elle est verticale, et d'équation x = x0.
[modifier] Interprétation mécanique
- Soit x(t) l'équation horaire d'un point matériel selon l'axe Ox en fonction du temps t. La limite
 est notée
est notée  et la fonction dérivée
et la fonction dérivée  est la vitesse du point, à l'instant t, selon l'axe Ox. L'accélération à l'instant t, selon ce même axe, est la dérivée seconde
est la vitesse du point, à l'instant t, selon l'axe Ox. L'accélération à l'instant t, selon ce même axe, est la dérivée seconde  . La loi fondamentale de la dynamique newtonienne s'exprime selon
. La loi fondamentale de la dynamique newtonienne s'exprime selon
 ,
,- où m est la masse de la particule considérée et Fx la composante, selon l'axe Ox, de la force qui s'exerce sur la particule, qui peut dépendre de
 . On obtient des équations différentielles que l'on ne sait résoudre analytiquement que pour des forces Fx assez simples.
. On obtient des équations différentielles que l'on ne sait résoudre analytiquement que pour des forces Fx assez simples.
[modifier] Interprétation chimique
- On considère un échantillon de matériau radio-actif qui contient N(t) atomes à l'instant N(t). La loi fondamentale qui régit l'évolution temporelle du phénomène de désintégration est la suivante: le taux de variation instantanée du nombre d'atomes est une constante négative, dont la valeur absolue est notée λ (elle varie selon la nature de l'atome). La variation instantanée du nombre d'atomes est la dérivée
 et le taux de variation est
et le taux de variation est  . On a donc pour loi de variation temporelle:
. On a donc pour loi de variation temporelle:
 .
.
- On obtient encore une équation différentielle; le lecteur peut vérifier que si N0 est le nombre d'atomes initial à t = 0, au temps t il n'en restera plus que N(t) = N0e − λt.
[modifier] Continuité et Dérivabilité
|
Théorème |
|
Toute fonction f dérivable en x0 est continue en ce point. |
Attention! La réciproque est fausse. Par exemple la fonction  est continue en x = 0, mais elle n'est pas dérivable en x = 0. Ici encore, prudence: il existe des fonctions continues sur
est continue en x = 0, mais elle n'est pas dérivable en x = 0. Ici encore, prudence: il existe des fonctions continues sur  qui ne sont dérivables en aucun point! On ne peut pas toujours "faire un dessin".
qui ne sont dérivables en aucun point! On ne peut pas toujours "faire un dessin".
[modifier] Calcul des dérivées
[modifier] Dérivées des fonctions composées
|
Théorème |
|
Si f est dérivable en g(x) et g est dérivable en x, alors fog est dérivable en x et |
Démonstration
- g dérivable en
 avec
avec  (1)
(1) - f dérivable en
![g(x) Leftrightarrow f[g(x)+h]=(f circ g)(x)+(f' circ g)(x)h+hepsilon_1(h)](http://upload.wikimedia.org/math/a/2/4/a2428e89016ec37de8256b76e7073e79.png) avec
avec  (2)
(2)
Nous devons montrer que 
Posons h' = g'(x)h + hε(h). Nous noterons (3) cette égalité. On a bien  .
.
![(f circ g)(x+h)=f[g(x+h)]=f[g(x)+g'(x)h+hepsilon(h)]](http://upload.wikimedia.org/math/9/7/c/97cde33500860cd6374f5e407374e65c.png) d'après (1)
d'après (1)
![=f[g(x)+h']=(f circ g)(x)+(f' circ g)(x)h'+h'epsilon_1(h)](http://upload.wikimedia.org/math/0/1/0/01052a2a445a7eaf0b3a43f0e5b53676.png) d'après (2)
d'après (2)
![=(f circ g)(x)+h[(f' circ g)(x)g'(x)]+h[(f' circ g)(x)epsilon(h)+epsilon_1(h)g'(x)+epsilon(h)epsilon_1(h)]](http://upload.wikimedia.org/math/2/8/7/2876114063dde12f5a67412e682a661a.png) d'après (3)
d'après (3)

Ainsi 
car  et on a bien
et on a bien  .
.
Remarque
Il existe une démonstration de ce théorème, apparemment plus simple, qui utilise l'"astuce"  , mais cette démonstration est moins bonne que la précédente car elle suppose que
, mais cette démonstration est moins bonne que la précédente car elle suppose que  pour tout x au voisinage de a, ce qui n'a aucune raison d'être !!!
pour tout x au voisinage de a, ce qui n'a aucune raison d'être !!!
[modifier] Dérivées des fonctions réciproques

[modifier] Différentielle
[modifier] Utilisations
[modifier] Dérivée première et variations
[modifier] Dérivée seconde et convexité
[modifier] Les théoremes fondamentaux
Étude de fonctions : Fonction dérivée
Étude de fonctions/Fonction dérivée
Une page de Wikiversité.
| Chapitre 6 | |||
| Leçon : Étude de fonctions | |||
|---|---|---|---|
| Chap. préc. : | Dérivation | ||
| Chap. suiv. : | Étude de fonctions | ||
Sommaire[masquer] |
[modifier] Définition
On dit qu'une fonction f est dérivable sur un intervalle I si et seulement si elle admet un nombre dérivé en tout nombre réel de I. La fonction qui à tout nombre réel x de I associe le nombre dérivé  est appelée fonction dérivée de f et est noté
est appelée fonction dérivée de f et est noté  .
.
[modifier] Écriture différentielle
Soit f une fonction dérivable sur un intervalle I et  sa fonction dérivée.
sa fonction dérivée.
 ,
,  avec
avec 
Posons  et
et  On a donc :
On a donc :



de plus  donc lorsque Δx devient infinitésimal, on écrit :
donc lorsque Δx devient infinitésimal, on écrit :  on note aussi :
on note aussi : 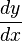
[modifier] Dérivées successives
Définition : Soit f une fonction dérivable sur un intervalle I. Si sa fonction dérivée  est dérivable sur cet intervalle I alors elle admet une fonction dérivée sur I appelée dérivée seconde de f et notée
est dérivable sur cet intervalle I alors elle admet une fonction dérivée sur I appelée dérivée seconde de f et notée  .
.
On dit alors que f est deux fois dérivable sur I. On peut ainsi définir les fonctions dérivées successives de f sur I si elles existent. On note f(3) la fonction dérivée troisième de f sur I. Pour tout entier n on note f(n) la dérivée n-ième avec  et
et  .
.
Avec la notation différentielle on écrit 
 ...
... 
[modifier] Opérations et dérivées
Soit u et v deux fonctions dérivables sur un intervalle I
| Opération | Dérivée |
|---|---|
| Somme |  |
| Produit |  |
| Produit par un réel |  |
| Carré d'une fonction |  |
| Cube d'une fonction |  |
Inverse   |
 |
Quotient   |
 |
Remarque : Les fonctions polynômes et rationnelles sont dérivables sur tout intervalle de  où elles sont définies
où elles sont définies
[modifier] Démonstration
Soit deux fonctions définies et dérivables sur  .
.
[modifier] Composée (théorème)
Soit f une fonction dérivable sur un intervalle I et g une fonction dérivable sur un intervalle J tel que  . Alors
. Alors  est dérivable sur I et on a
est dérivable sur I et on a 
[modifier] Démonstration
![frac{left(g circ fright)(a + h) - left(g circ fright)(a)}{h} = frac{gleft[f(a + h)right] - gleft[f(a)right]}{h} = T(h)](http://upload.wikimedia.org/math/7/1/7/7176a7f083d9b46faca70bfcfa214097.png)
![approx frac{gleft[f(a) + hf^{prime}(a) + hphi(h)right] - gleft[f(a)right)]}{h} times frac{f^{prime}(a)}{f^{prime}(a)}](http://upload.wikimedia.org/math/c/9/d/c9d8928ceaf4ef9853689c8843895a77.png)
![approx frac{gleft[f(a) + hf^{prime}(a)right] - gleft[f(a)right]}{hf^{prime}(a)} times f^{prime}(a)](http://upload.wikimedia.org/math/0/0/f/00fa4765320c3aa721f39a6b2d904e13.png)
or 
donc ![lim_{h to 0}T(h) = g^{prime}[f(a)] times f^{prime}(a)](http://upload.wikimedia.org/math/a/7/5/a75ec66a9ef5136c7dde3a8e0d5653a7.png)
donc ![(g circ f)^{prime} = g^{prime}[f(a)] times f^{prime}(a)](http://upload.wikimedia.org/math/7/f/7/7f765414174f1d7d5ddc76343b0432f8.png)
[modifier] Corollaire
Soit u une fonction dérivable sur un intervalle I. Pour tout entier naturel n 
 .
.
Si u est strictement positive sur I 
[modifier] Sens de variation (théorème)
Soit une fonction f définie et dérivable sur un intervalle I.
- Si pour tout
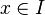 on a
on a  alors f est croissante sur I.
alors f est croissante sur I.
- Si pour tout
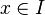 on a
on a  alors f est décroissante sur I.
alors f est décroissante sur I.
- Si pour tout
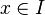 on a
on a  alors f est strictement croissante sur I.
alors f est strictement croissante sur I.
- Si pour tout
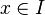 on a
on a  alors f est strictement décroissante sur I.
alors f est strictement décroissante sur I.
[modifier] Extremum local (théorème)
Soit une fonction f définie et dérivable sur un intervalle I de  et x0 un nombre de I. Si f admet un extremum local en x0 alors
et x0 un nombre de I. Si f admet un extremum local en x0 alors  .
.
[modifier] Tableau des dérivés
 |
|
 |
|
 |
|
 |
|
 |
|
| u > 0 |  |
Soit  Soit  et et  Soit  et et 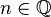 |
 |
 avec avec  |
 |
 |
|
 |
Étude de fonctions : Étude de fonctions
Étude de fonctions/Étude de fonctions
Une page de Wikiversité.
| Chapitre 7 | |||
| Leçon : Étude de fonctions | |||
|---|---|---|---|
| Chap. préc. : | Fonction dérivée | ||
[modifier] Introduction
L'étude de fonctions est une synthèse de toutes les notions entourant les fonctions. Il s'agit, à partir d'une expression donnée, de connaître son comportement et sa nature de manière théorique. L'étude d'une fonction a de nombreuses applications, elle s'applique à l'économie pour calculer le rendement de la production d'un produit, en physique pour étudier un phénomène en fonction du temps, de l'espace, en biologie, et dans de nombreux autres domaines. Nous allons dans la suite progresser en détaillant précisément le plan d'étude d'une application nommée f.
[modifier] Caractérisation
L'étude suit un plan logique et rigoureux.
- Toute application a un domaine de définition:
 , ou tout intervalle réel. Ce domaine correspond à l'ensemble des points où la valeur f(x) existe (par exemple, la fonction inverse n'est pas définie en 0).
, ou tout intervalle réel. Ce domaine correspond à l'ensemble des points où la valeur f(x) existe (par exemple, la fonction inverse n'est pas définie en 0). - Elle a aussi un domaine de continuité en montrant que pour tout point du domaine l'application est continue: on utilise ici les limites en montrant que pour tout élément x0 de l'ensemble on a :

- On cherche ensuite à simplifier l'étude, en étudiant la parité ou la périodicité de l'application.
Parité: on regarde (c'est important) d'abord si l'ensemble de définition est symétrique par rapport à l'origine. Ensuite on cherche f(-x), on regarde si c'est égal à -f(x) (fonction impaire) ou à f(x) (fonction paire). Attention, cette recherche doit être effectuée seulement si la parité paraît plausible (si f(x)= exp(x) ce n'est pas utile: e − x = 1 / ex). L'existence d'une parité permet de n'étudier la fonction que pour les réels positifs, et d'en déduire les variations pur x négatif. Périodicité: on cherche un réel T tel que f(x+T)=f(x) ou plus généralement f(x+kT)=f(x) où k est un entier relatif. Ici aussi, il ne faut pas chercher inutilement ce genre de simplification. Le cas le plus courant (98% des cas) concerne les fonctions trigonométriques (cosinus, sinus, ...). De même, cette simplification permet d'étudier f sur un intervalle [x;x+T].
- On détermine ensuite le domaine de dérivabilité, en utilisant les propriétés de dérivation usuelles.
- On dérive ensuite la fonction, en utilisant les règles usuelles.
- On en déduit les variations suivant le signe de la dérivée (cela nécessite parfois un deuxième calcul de dérivée).
- On calcule ensuite les limites aux bornes de l'ensemble de continuité/dérivation, pour la fonction et sa dérivée (couramment en
 , et parfois en un point où f (ou f') n'est pas continue.
, et parfois en un point où f (ou f') n'est pas continue.
Prochains développements (en cours d'écriture):
- On cherche et calcule les valeurs remarquables: en plus des limites, il est parfois utile de calculer f(x) pour certaines valeurs de x, comme zéro pour les fonctions paires et impaires, ou pour les x où f(x)=0 si on vous le demande,...
- Enfin, il est parfois demandé (ou utile) de déterminer les asymptotes. Celles-ci se calculent en l'infini, et plus généralement aux bornes du domaine de continuité (la fonction inverse possède une asymptote verticale x=0.
Cette étude permet de dresser le tableau de variations qui récapitule toute l'étude. Un exemple d'étude de fonction se trouve ici:
Exercice : Fonctions associées
Étude de fonctions/Exercices/Fonctions associées
Une page de Wikiversité.
| Exercice | |||
| Leçon : Étude de fonctions | |||
|---|---|---|---|
|
Cet exercice est de niveau 11. |
|||
[modifier] Exercice 1
Soit u une fonction définie sur ![[-3;5],](http://upload.wikimedia.org/math/9/9/4/994d581afac61eea6b452df2412f1c65.png) dont on donne le tableau de variation :
dont on donne le tableau de variation :

Déterminer le tableau de variation des fonctions suivantes :
[modifier] Exercice 2
On pose les fonctions ƒ et u, définies sur  par :
par :
On note  et
et  les courbes représentatives de ƒ et u dans un repère orthonormé
les courbes représentatives de ƒ et u dans un repère orthonormé  donné.
donné.
- 1. Pour tout x, écrire ƒ(x) en utilisant u.
- 2. Donner les transformations qui permettent d'obtenir
 à partir de
à partir de 
- 3. Dresser le tableau de variation de ƒ.






 et finalement
et finalement  .
. .
.






 .
.








 la fonction dérivée
la fonction dérivée  .
. signifie simplement que
signifie simplement que  , avec les polynômes, l'exponentielle, le sinus, le cosinus et la gaussienne
, avec les polynômes, l'exponentielle, le sinus, le cosinus et la gaussienne  avec
avec  .
.



 :
:
 :
:
 :
:
 :
:
 :
:






 , puis
, puis  et enfin
et enfin  .
.


