Fonction dérivée : Nombre dérivé
Fonction dérivée/Nombre dérivé
Une page de Wikiversité.
| Chapitre 1 | |||
| Leçon : Fonction dérivée | |||
|---|---|---|---|
| Retour au | Sommaire | ||
| Chap. suiv. : | Équation d'une tangente | ||
Sommaire[masquer] |
[modifier] Accroissement d'une fonction affine
Soit une fonction affine ƒ définie sur  par
par  .
.
a est appelé le coefficient directeur de ƒ.
Pour déterminer ce coefficient directeur à partir de la représentation graphique de la fonction,
on choisit deux points du graphe et on mesure (cf. figure ci-contre) :
- la différence des abscisses Δx
- la différence des ordonnées Δy
On a alors 
La grandeur a caractérise la pente de la droite :
plus a est grand et plus la droite monte vite.
On appelle donc également a accroissement de la fonction ƒ.
[modifier] Accroissement moyen
[modifier] Introduction
Dans le cas d'une fonction  quelconque, définie sur un intervalle I, (voir figure ci-contre), l'accroissement de la fonction n'est pas constant. Parfois la fonction monte, parfois elle redescend, plus ou moins vite. On ne peut pas travailler aussi simplement qu'avec les fonctions affines.
quelconque, définie sur un intervalle I, (voir figure ci-contre), l'accroissement de la fonction n'est pas constant. Parfois la fonction monte, parfois elle redescend, plus ou moins vite. On ne peut pas travailler aussi simplement qu'avec les fonctions affines.
On introduit donc la notion d'accroissement moyen sur un intervalle.
|
Définition |
|
Soient On note A et B les points de la courbe représentative de ƒ dans un repère
Son coefficient directeur vaut : |
Voyons sur quelques exemples l'utilité de l'accroissement moyen d'une fonction entre deux points.
[modifier] Exemple 1
Un véhicule parcourt 1000 km en 10 h. Quelle est sa vitesse moyenne ?

La vitesse moyenne est l'accroissement moyen de la fonction qui donne la distance parcourue en fonction du temps entre le départ et l'arrivée.
[modifier] Exemple 2
Un pays produit annuellement 1000 tonnes de blé en l'an 1900 et 10000 tonnes de blé en l'an 2000. De combien de tonnes la production a-t-elle augmenté en moyenne par an ?
[modifier] Nombre dérivé d'une fonction en x = a
[modifier] Introduction
L'accroissement moyen d'une fonction sur un intervalle peut être utile pour une première approche, mais n'est pas forcément représentatif du comportement de la fonction sur cet intervalle. Prenons l'exemple de la fonction ci-dessous :
Entre A et B, les variations de la fonction sont beaucoup plus brutales que ne le laisse apparaître l'accroissement moyen. L'idéal serait de disposer d'un outil plus fin qui rendrait compte de l'accroissement en chaque point. Géométriquement, un tel outil existe : il s'agit de la tangente à une courbe en un point.
Le coefficient directeur de la tangente en un point A est ici la grandeur qui nous intéresse le plus, car il correspond à l'accroissement de la fonction au point A d'abscisse a.
Ce qu'on cherche à faire est donc : trouver un outil permettant d'obtenir l'accroissement d'une fonction, c'est-à-dire le coefficient directeur de la tangente à sa courbe, en tout point de l'intervalle de définition.
[modifier] Définition du nombre dérivé
Soit 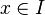
On cherche à trouver le coefficient directeur de la tangente à la courbe de ƒ au point d'abscisse x.
Pour ce faire, on réutilise la notion d'accroissement sur un intervalle ![[x;x+h],](http://upload.wikimedia.org/math/a/2/a/a2a26715d4b3799e8e55373061610228.png) où
où  .
.
L'accroissement moyen de ƒ sur l'intervalle ![[x;x+h],](http://upload.wikimedia.org/math/a/2/a/a2a26715d4b3799e8e55373061610228.png) vaut
vaut 
Comme ce qui nous intéresse est la tangente, et non une corde, on va diminuer h. Cette manipulation a pour effet de rapprocher les deux points A et B. On s'aperçoit alors que, ce faisant, la corde (AB) se rapproche de plus en plus de la position de la tangente en A à la courbe de ƒ.
Ainsi, lorsque h devient extrêmement petit :
- (AB) se confond avec la tangente en A à la courbe de ƒ
- l'accroissement moyen de ƒ sur l'intervalle
![[x;x+h],](http://upload.wikimedia.org/math/a/2/a/a2a26715d4b3799e8e55373061610228.png) vaut le coefficient directeur de la tangente en A à la courbe de ƒ
vaut le coefficient directeur de la tangente en A à la courbe de ƒ
On introduit ainsi la notion de nombre dérivé :
|
Définition |
|
La limite de l'accroissement moyen de ƒ entre
|
|
Notation en physique |
|
En mathématiques, on utilise la notation avec une prime pour désigner la dérivée. En physique, on utilise plus couramment une autre notation, appelée notation différentielle. On note Le symbole « petit d » en physique signifie une petite variation de la grandeur qui suit le d. La notation
|
[modifier] Interprétation graphique
|
Propriété |
|
|
[modifier] Restrictions
Nous verrons par la suite que le nombre dérivé n'est pas toujours défini.
|
Définition |
|
Si, en un point |
[modifier] Notes
- ↑ ƒ '(a) se lit « f prime de a »
Fonction dérivée : Fonction dérivée
Fonction dérivée/Fonction dérivée
Une page de Wikiversité.
| Chapitre 3 | |||
| Leçon : Fonction dérivée | |||
|---|---|---|---|
| Chap. préc. : | Équation d'une tangente | ||
| Chap. suiv. : | Dérivée et variations | ||
Sommaire[masquer] |
[modifier] Définition
Soit ƒ une fonction définie sur un intervalle I à valeurs dans 
|
Dérivabilité |
|
On dit que ƒ est dérivable sur I si, pour tout |
Supposons maintenant ƒ dérivable sur I. On peut alors définir la fonction dérivée de ƒ.
|
Fonction dérivée |
|
La fonction dérivée de ƒ, notée
|
[modifier] Calcul basique
Dans ce paragraphe, on montre comment calculer à partir de la définition la fonction dérivée d'une fonction donnée sur l'exemple de la fonction carré.
|
Exemple |
|
On considère la fonction Soit Soit Le nombre dérivé de ƒ en a est donc On en déduit que la fonction dérivée de |
On voit bien que cette méthode induit rapidement de gros calculs, aussi par la suite on apprendra une table des dérivées pour les fonctions les plus couramment employées afin d'éviter cette corvée.
[modifier] Dérivées des fonctions usuelles
[modifier] Fonctions ƒ : x → xn avec n ∈ Z*
|
Théorème |
|
Soit La fonction Pour tout |
|
Quelques dérivées de fonctions de la forme x → xn |
|
|
[modifier] Tableau récapitulatif des dérivées usuelles
Soit 
Soient  et
et 
| f(x) | f'(x) | Intervalle de dérivabilité |
|---|---|---|
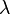 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
si 
si |
 |
 |
 |
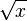 |
 |
![]0;+infty[](http://upload.wikimedia.org/math/a/b/e/abe7a92275e0c5644d5bd5c819fa694e.png) |
 |
 |
 |
 |
 |
 |
Fonction dérivée : Dérivée d'un produit
Fonction dérivée/Dérivée d'un produit
Une page de Wikiversité.
| Chapitre 6 | |||
| Leçon : Fonction dérivée | |||
|---|---|---|---|
| Chap. préc. : | Extremum local | ||
| Chap. suiv. : | Dérivée de la puissance énième d'une fonction | ||
Sommaire[masquer] |
[modifier] Dérivée d'une fonction puissance
|
Théorème |
|
La dérivée de la fonction |
[modifier] Exemples
- ƒ est dérivable sur
 et, pour tout
et, pour tout 

- ƒ est dérivable sur
 et, pour tout
et, pour tout 

- ƒ est dérivable sur
 et, pour tout
et, pour tout 

- ƒ est dérivable sur
 et, pour tout
et, pour tout 

[modifier] Dérivée d'un produit
|
Théorème |
|
La dérivée d'une fonction produit |
[modifier] Exemples
- ƒ est dérivable sur
 et, pour tout
et, pour tout 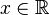 :
: 
- ƒ est dérivable sur
 et, pour tout
et, pour tout 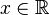 :
:

[modifier] Avec des racines carrées
|
Théorème |
|
Rappel : La dérivée de La fonction racine carrée est dérivable sur |
- ƒ est dérivable sur
![]0;+infty[](http://upload.wikimedia.org/math/a/b/e/abe7a92275e0c5644d5bd5c819fa694e.png) et, pour tout
et, pour tout ![xin]0;+infty[](http://upload.wikimedia.org/math/1/3/2/132576a4ec9b669dca74efcc85c5b79f.png)

Fonction dérivée : Dérivée d'un quotient
Fonction dérivée/Dérivée d'un quotient
Une page de Wikiversité.
| Chapitre 8 | |||
| Leçon : Fonction dérivée | |||
|---|---|---|---|
| Chap. préc. : | Dérivée de la puissance énième d'une fonction | ||
| Chap. suiv. : | Dérivée d'une fonction affine suivie d'une autre fonction | ||
Sommaire[masquer] |
[modifier] Dérivée d'un inverse
|
Théorème |
|
Soit u une fonction dérivable et ne s'annulant pas sur un domaine I. La dérivée de la fonction |
|
Dérivée de la fonction inverse |
|
[modifier] Exemple 1
On souhaite dériver la fonction  , définie sur
, définie sur 
Pour tout 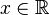 :
:
[modifier] Exemple 2
On souhaite dériver la fonction  , définie sur
, définie sur 
Pour tout  :
:
[modifier] Dérivée d'un quotient
|
Théorème |
|
Soient u et v deux fonctions dérivables sur un domaine D. La dérivée de la fonction |
[modifier] Exemple 1
- On souhaite dériver la fonction
 définie sur
définie sur 
Pour tout 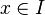 :
:
[modifier] Exemple 2
On souhaite dériver la fonction  , définie sur
, définie sur ![I=Rbackslashleft{sqrt[3]{frac52}right}](http://upload.wikimedia.org/math/3/b/4/3b462d009c52deb699e353f564ed4b0c.png)
Pour tout 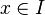 :
:
Fonction dérivée : Dérivée et variations
Fonction dérivée/Dérivée et variations
Une page de Wikiversité.
| Chapitre 4 | |||
| Leçon : Fonction dérivée | |||
|---|---|---|---|
| Chap. préc. : | Fonction dérivée | ||
| Chap. suiv. : | Extremum local | ||
Sommaire[masquer] |
[modifier] Sens de variation
[modifier] Lien entre nombre dérivé et sens de variation
Soit ƒ une fonction dérivable sur son intervalle de définition I.
On a vu que, en tout point  est le coefficient directeur de la tangente à la courbe de ƒ dans un repère. De cette propriété, on voit émerger la constatation suivante :
est le coefficient directeur de la tangente à la courbe de ƒ dans un repère. De cette propriété, on voit émerger la constatation suivante :
- Si
 , la tangente à la courbe de ƒ en a est croissante. Cela induit que, sur une petite zone autour de a, la courbe de ƒ est nécessairement croissante pour pouvoir être tangente à la droite.
, la tangente à la courbe de ƒ en a est croissante. Cela induit que, sur une petite zone autour de a, la courbe de ƒ est nécessairement croissante pour pouvoir être tangente à la droite. - Au contraire, si
 la tangente est décroissante. La courbe de ƒ doit alors nécessairement être décroissante sur une petite zone autour de a pour pouvoir satisfaire à la même propriété.
la tangente est décroissante. La courbe de ƒ doit alors nécessairement être décroissante sur une petite zone autour de a pour pouvoir satisfaire à la même propriété.
[modifier] Théorème global
|
Théorème |
|
Soit ƒ une fonction dérivable sur un intervalle I.
|
On s'intéresse à présent à la stricte croissance de ƒ sur l'intervalle I. Pour cela, il faut remarquer que, si en un point  , la tangente à la courbe de ƒ est une droite horizontale.
, la tangente à la courbe de ƒ est une droite horizontale.
La fonction ƒ ne sera pas strictement croissante s'il existe des intervalles non réduits à un point où ƒ reste constante, c'est-à-dire s'il n'existe que quelques points isolés où ƒ' s'annule.
|
Théorème |
|
Soit ƒ une fonction dérivable sur un intervalle I
|
[modifier] Exemples
Vérifier ce théorème sur les fonctions usuelles sur des intervalles convenables.
[modifier] Exercices
- Montrer sur un exemple simple que la réciproque du théorème « strict » est fausse si on enlève la précision : « sauf en un nombre fini de points ».
- Étudier les variations de la fonction trinôme

[modifier] Tableaux de variations
Pour mettre en relation le signe de la dérivée et les variations d'une fonction,
on utilise un tableau de signe et variations comme ci-dessous :

- Remarques
- Noter la différence de légende : on parle du signe de
 et des variations de la fonction
et des variations de la fonction  .
. - Les flèches désignent conventionnellement sauf indication contraire des croissances et décroissances strictes.
Fonction dérivée : Dérivée d'une fonction composée
Fonction dérivée/Dérivée d'une fonction composée
Une page de Wikiversité.
| Chapitre 10 | |||
| Leçon : Fonction dérivée | |||
|---|---|---|---|
| Chap. préc. : | Dérivée d'une fonction affine suivie d'une autre fonction | ||
Sommaire[masquer] |
[modifier] Dérivée d'une fonction composée
[modifier] Théorème
On s'intéresse dans ce chapitre à la dérivation d'une fonction dont l'expression à partir d'un réel x est obtenue en deux temps :
- On applique d'abord une fonction ƒ à x
- On applique ensuite au résultat une autre fonction g
Le schéma étudié est donc le suivant :
qui peut se ramener à l'étude de
|
Théorème |
|
Si alors la composée
|
| Lorsqu'on utilise ce genre de théorème, il faut être particulièrement vigilant aux domaines de définition et de dérivabilité. Nous allons le voir sur quelques exemples. |
[modifier] Exemple 1
|
Exemple |
|
Soit h la fonction définie sur |
|
Méthode de dérivation |
|
Le schéma est
et se ramène à
Les deux fonctions mises en jeu sont alors :
On a bien 
- ƒ est définie et dérivable sur
 et, pour tout
et, pour tout 
- g est définie et dérivable sur
 et
et  et, pour tout
et, pour tout 
- On applique la formule du théorème :
- Pour tout
 :
: 
Finalement, pour tout  |
[modifier] Exemple 2
|
Exemple |
|
Soit h la fonction définie par
|
- Domaine de définition
Une racine carrée est définie si et seulement si son contenu est positif.
Une étude de la fonction du second degré  donne le tableau de signes suivant :
donne le tableau de signes suivant :

 Pour des rappels sur la résolution des inéquations du second degré, se reporter au cours sur les fonctions et équations du second degré.
Pour des rappels sur la résolution des inéquations du second degré, se reporter au cours sur les fonctions et équations du second degré.
Donc h est définie sur ![mathcal D=]-infty;1]cup[2;+infty[](http://upload.wikimedia.org/math/e/d/c/edc63da43a967042c056acdc3e1bd899.png) |
- Étude de la dérivabilité
Le schéma est
et se ramène à
Les deux fonctions mises en jeu sont alors :
On a bien 
- ƒ est définie et dérivable sur
 et, pour tout
et, pour tout 
- g est définie sur
 , mais n'est dérivable que sur
, mais n'est dérivable que sur 
- Pour avoir la dérivabilité de
 , il faut donc retirer tous les points pour lesquels
, il faut donc retirer tous les points pour lesquels  , c'est-à-dire 1 et 2.
, c'est-à-dire 1 et 2.
Au total,  est dérivable sur est dérivable sur ![mathcal D'=]-infty;1color{red}[color{black}cupcolor{red}]color{black}2;+infty[](http://upload.wikimedia.org/math/e/3/d/e3d27d46b48910a53d8d7b88e496c9da.png) |
- On applique la formule du théorème :
- Pour tout
 :
: 
Finalement, pour tout  |
[modifier] Autres exemples
Dériver les fonctions suivantes en utilisant la formule de composition en précisant le domaine sur lequel cette dérivation est valable.
[modifier] Conséquences : Formules de dérivation
Soit u une fonction définie sur un domaine  à valeurs dans
à valeurs dans 
On obtient les formules de dérivation de composées suivantes :

Si de plus, pour tout 





 .
. qui ont pour abscisses respectives a et b:
qui ont pour abscisses respectives a et b:

 ,
, et s'appelle accroissement moyen de ƒ entre a et b
et s'appelle accroissement moyen de ƒ entre a et b








 lorsque
lorsque 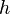 tend vers 0 est appelée nombre dérivé de ƒ en
tend vers 0 est appelée nombre dérivé de ƒ en  et noté
et noté 
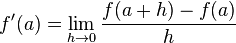
 .
. signifie donc qu'on considère :
signifie donc qu'on considère : lorsque
lorsque  )
) lorsque
lorsque 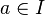 , ƒ est dérivable en a, c'est-à-dire que le nombre dérivé de ƒ en a (noté ƒ'(a)) existe.
, ƒ est dérivable en a, c'est-à-dire que le nombre dérivé de ƒ en a (noté ƒ'(a)) existe. ,est la fonction qui, à chaque
,est la fonction qui, à chaque 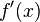 .
.

 , dont on admet la dérivabilité sur
, dont on admet la dérivabilité sur 

 , et ce pour tout
, et ce pour tout  .
. est dérivable sur
est dérivable sur 





 est
est 








![f'left(-frac32right)=27left[left(-frac32right)^2right]^{13} =27frac{9^{13}}{4^{13}}](http://upload.wikimedia.org/math/4/1/a/41a44750fdc5a09ae466d349bc1fae44.png)



 est :
est : 




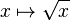 est
est 


 est définie sur I par l'expression
est définie sur I par l'expression 
 de la fonction inverse
de la fonction inverse  est
est 










![color{red}]color{black}0;+infty[](http://upload.wikimedia.org/math/7/3/f/73f2aa4b7083037eba23157990529ee5.png) et, pour tout
et, pour tout ![xin color{red}]color{black}0;+infty[](http://upload.wikimedia.org/math/3/3/7/337ab1d0c589d4cf829b65c44574751d.png) :
:


 est définie sur D privé des points où v s'annule par l'expression
est définie sur D privé des points où v s'annule par l'expression 




 et
et 




 et
et 






 sauf peut-être en un nombre fini de points où
sauf peut-être en un nombre fini de points où  sauf peut-être en un nombre fini de points où
sauf peut-être en un nombre fini de points où 


![xin ]0;+infty[,~f'(x)=frac1{2sqrt x}](http://upload.wikimedia.org/math/a/3/b/a3bcc514b78211cd690acb3a0a65057b.png)






![left]frac34;+inftyright[](http://upload.wikimedia.org/math/c/e/e/ceed8fe9ca26be17d1af2f672dfedd00.png)
![left]-infty;frac34right[](http://upload.wikimedia.org/math/c/8/e/c8e4138bf0ceea8932fc52b4b8b3fb56.png)



 et
et  est dérivable sur
est dérivable sur 
 est dérivable sur
est dérivable sur  .
. :
:


 avec
avec  (1)
(1)![g(x) Leftrightarrow f[g(x)+h]=(fog)(x)+(f'og)(x)h+hepsilon_1(h)](http://upload.wikimedia.org/math/c/7/4/c743d67f3d16a29b62c883d7ebb2b6fb.png) avec
avec 
 .
.
 ).
). . Dériver h
. Dériver h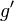




 .
. de h
de h




 montre que, pour tout
montre que, pour tout 





 , mais n'est dérivable que sur
, mais n'est dérivable que sur  ne s'annule pas sur
ne s'annule pas sur 









 , c'est-à-dire
, c'est-à-dire 
 :
:

 .
. avec
avec  .
.

