Fonction exponentielle : L'exponentielle comme solution d'une équation différentielle
Fonction exponentielle/L'exponentielle comme solution d'une équation différentielle
Une page de Wikiversité.
| Chapitre 1 | |||
| Leçon : Fonction exponentielle | |||
|---|---|---|---|
| Retour au | Sommaire | ||
| Chap. suiv. : | L'exponentielle comme fonction réciproque du logarithme népérien | ||
Sommaire[masquer] |
[modifier] Exponentielle et équation différentielle
|
Définition |
|
Il existe une unique fonction dérivable de
Autrement dit, l'exponentielle est la seule fonction qui est égale à sa propre dérivée valant 1 en 0. |
[modifier] Calculatrice
Pour prendre l'exponentielle d'un nombre, on utilise la touche « ex ».
On effectue souvent cette opération en utilisant le préfixe « seconde » ou « shift » suivi de la touche ln.
[modifier] Exemples
[modifier] Cas général
|
Théorème |
|
Pour tout réel k, il existe une unique fonction dérivable sur Cette fonction est |
Fonction exponentielle : Propriétés algébriques de l'exponentielle
Fonction exponentielle/Propriétés algébriques de l'exponentielle
Une page de Wikiversité.
| Chapitre 3 | |||
| Leçon : Fonction exponentielle | |||
|---|---|---|---|
| Chap. préc. : | L'exponentielle comme fonction réciproque du logarithme népérien | ||
| Chap. suiv. : | Étude de la fonction exponentielle | ||
Sommaire[masquer] |
[modifier] Propriété fondamentale
|
Propriété |
alors |
[modifier] Conséquences
On utilisera souvent les formules suivantes qui se déduisent de la propriété algébrique fondamentale.
|
Propriété |
|
[modifier] Notation
|
Notation |
|
On peut adopter une notation de la fonction exponentielle sous la forme d'une puissance :
L’exponentielle se comporte comme si on « prenait » les puissances de e,
|
 est donc simplement e au carré
est donc simplement e au carré
mais l’exponentielle nous permet de donner un sens à  par exemple.
par exemple.
[modifier] Application
- Soit x tel que ex = 3,56. Calculer e2x+3 sans calculer x.
- Déterminer une valeur approchée de
 sans utiliser la touche « ex » de la calculatrice.
sans utiliser la touche « ex » de la calculatrice.
Fonction exponentielle : Étude de la fonction exponentielle
Fonction exponentielle/Étude de la fonction exponentielle
Une page de Wikiversité.
| Chapitre 4 | |||
| Leçon : Fonction exponentielle | |||
|---|---|---|---|
| Chap. préc. : | Propriétés algébriques de l'exponentielle | ||
| Chap. suiv. : | Croissances comparées | ||
Sommaire[masquer] |
[modifier] Dérivée de la fonction exponentielle
|
Théorème |
|
La dérivée de la fonction |
[modifier] Variations de la fonction exponentielle
[modifier] Positivité de l'exponentielle
|
Propriété |
|
Pour tout |
[modifier] Variations de la fonction exponentielle
|
Théorème |
|
La fonction exponentielle est strictement croissante sur |
[modifier] Limites aux bornes
[modifier] Limite en + ∞
|
Théorème |
|
|
[modifier] Limite en -∞
|
Théorème |
|
|
[modifier] Courbe représentative
On a tracé ci-dessous la courbe de la fonction exponentielle.
[modifier] Tangente remarquable
|
Propriété |
|
Au point (0 ; 1), la tangente a pour équation on peut donc donner une approximation affine de exp au voisinage de 0 : |
Fonction exponentielle : Dérivée de exp(u)
Fonction exponentielle/Dérivée de exp(u)
Une page de Wikiversité.
| Chapitre 6 | |||
| Leçon : Fonction exponentielle | |||
|---|---|---|---|
| Chap. préc. : | Croissances comparées | ||
| Chap. suiv. : | Exponentielle de base a | ||
Sommaire[masquer] |
[modifier] Dérivée de x → eax+b
On considère des fonctions de la forme  .
.
Par exemple, soit la fonction ƒ définie par :
- pour tout
 .
.
ƒ est la fonction composée de la fonction affine
 , définie sur
, définie sur 
et de la fonction exponentielle, ce que l’on représente par le schéma :

Pour calculer l'expression de ƒ', on utilise le théorème suivant :
|
Théorème |
|
Soient a et b deux réels. Soit g une fonction définie par Si ƒ est dérivable au point d'abscisse x alors g est dérivable au point d'abscisse a x + b et : pour tout |
Dans notre cas particulier
- pour tout

[modifier] Dérivée de eu
Toujours dans l'exemple de la fonction ƒ, on avait pour tout  .
.
On généralise ce procédé au cas où u n’est pas forcément affine.
|
Théorème |
|
Soit u une fonction dérivable sur un intervalle I. Alors eu est dérivable sur I et :  |
[modifier] Exemples
Sans se préoccuper de l’intervalle I, dériver les fonctions ƒ suivantes :
[modifier] Exemple 1

- Pour tout

- Pour tout

- Donc pour tout

[modifier] Exemple 2

[modifier] Exemple 3

[modifier] Exemple 4

[modifier] Exemple 5

[modifier] Exemple 6

[modifier] Exemple : l’exponentielle décroissante
On considère la fonction définie sur  par
par  .
.
On a alors pour tout  et le tableau de variations :
et le tableau de variations :
| x | |
| ƒ' | |
| ƒ |
Les limites aux bornes sont :
Exercice : Propriétés algébriques de l'exponentielle
Fonction exponentielle/Exercice/Propriétés algébriques de l'exponentielle
Une page de Wikiversité.
| Exercice 3 | |||
| Leçon : Fonction exponentielle | |||
|---|---|---|---|
|
Cet exercice est de niveau 12. |
|||
Sommaire[masquer] |
[modifier] Exercice 1
Soit 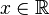 . Dans chaque cas, simplifier l'expression:
. Dans chaque cas, simplifier l'expression:
[modifier] Exercice 2
Soit 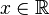 . Dans chaque cas, mettre sous la forme d'une seule exponentielle :
. Dans chaque cas, mettre sous la forme d'une seule exponentielle :
[modifier] Exercice 3
Soit 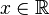 . Dans chaque cas, mettre sous la forme d'une seule exponentielle :
. Dans chaque cas, mettre sous la forme d'une seule exponentielle :
[modifier] Exercice 4
Démontrer que pour tout réel x :
[modifier] Exercice 5
Démontrer que pour tout réel x :
Exercice : Équations comportant des exponentielles
Fonction exponentielle/Exercice/Équations comportant des exponentielles
Une page de Wikiversité.
| Exercice 1 | |||
| Leçon : Fonction exponentielle | |||
|---|---|---|---|
| Chapitre du cours : | Fonction exponentielle | ||
|
Cet exercice est de niveau 12. |
|||
Objectif : On se propose de résoudre un certain nombre d'équations où l'inconnue x est toujours "dans une exponentielle".
Principe général : On change d'inconnue en posant  , on résout en X puis avec
, on résout en X puis avec  , on revient à l'inconnue de départ x.
, on revient à l'inconnue de départ x.
Sommaire[masquer] |
[modifier] Équations se ramenant au premier degré
[modifier] Exemple
Résoudre dans  l'équation
l'équation 
[modifier] Exercice
Résoudre dans  l'équation
l'équation 
[modifier] Équations se ramenant au second degré
[modifier] Exemple
Résoudre dans  l'équation
l'équation  .
.
[modifier] Exercices
- Résoudre dans
 l'équation
l'équation 
- Résoudre dans
 l'équation
l'équation 
- Résoudre dans
 l'équation
l'équation 
- Résoudre dans
 l'équation
l'équation 
NB : il faut garder à l'esprit que X devra être positif pour pouvoir trouver des solutions car c'est une exponentielle.
[modifier] Système avec exponentielles se ramenant à des systèmes linéaires
[modifier] Exercice
- Résoudre

ercice : Étude de la fonction exponentielle
Fonction exponentielle/Exercice/Étude de la fonction exponentielle
Une page de Wikiversité.
| Exercice 4 | |||
| Leçon : Fonction exponentielle | |||
|---|---|---|---|
|
Cet exercice est de niveau 12. |
|||
Un certain nombre d'études de fonctions ne peuvent se faire sans le théorème de dérivation d'une composée par une fonction affine (niveau 11).
Sommaire[masquer] |
[modifier] Exercice 1
ƒ est la fonction définie sur  par :
par :
- pour tout
 .
.
1. Étudier les variations de ƒ.
2. Étudier la limite de ƒ en  .
.
3. Démontrer que la courbe représentative 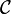 de ƒ admet une asymptote oblique
de ƒ admet une asymptote oblique  dont on donnera une équation.
dont on donnera une équation.
4. Étudier les positions relatives de 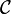 et
et  .
.
5. Déterminer une équation de la tangente à 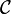 au point d'abscisse 2.
au point d'abscisse 2.
[modifier] Exercice 2
ƒ est la fonction définie sur  par :
par :
- pour tout
 .
.
1. Étudier les variations de ƒ.
2. Étudier la limite de ƒ en  .
.
3. Démontrer que la courbe représentative 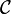 de ƒ admet une asymptote oblique
de ƒ admet une asymptote oblique  dont on donnera une équation.
dont on donnera une équation.
4. Étudier les positions relatives de 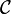 et
et  .
.
5. Déterminer une équation de la tangente à 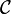 au point d'abscisse 2.
au point d'abscisse 2.
[modifier] Exercice 3
Calculer la fonction dérivée des fonctions suivantes.
1. 
2. 
3. 
[modifier] Exercice 4
Calculer la fonction dérivée des fonctions suivantes.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
[modifier] Exercice 5
Pour tout réel λ > 0, on note ƒλ la fonction définie sur  par :
par :
- pour tout

1. Tracer sur calculatrice la courbe représentative de ƒλ pour λ = 0,5 et pour λ = 3.
2. Démontrer que ƒλ est paire, c'est-à-dire pour tout  .
.
3. Étudier les variations de ƒλ et déterminer sa limite en  .
.
Exercice : Désintégration des corps radioactifs
Fonction exponentielle/Exercice/Désintégration des corps radioactifs
Une page de Wikiversité.
| Exercice 5 | |||
| Leçon : Fonction exponentielle | |||
|---|---|---|---|
| Chapitre du cours : | Fonction exponentielle | ||
|
Cet exercice est de niveau 12. |
|||
La « vitesse de désintégration » d'un corps radioactif, c'est-à-dire le nombre de noyaux qui se désintègrent pendant une seconde,
est proportionnelle au nombre de noyaux N(t) présent à l'instant t.
On peut donc écrire :

où λ est une constante strictement positive, caractéristique du noyau étudié.
[modifier] La loi de désintégration
On note N0 le nombre de noyaux d'un échantillon du corps radioactif à l'instant t = 0.
Montrer que pour tout réel t,  .
.
C'est la loi de désintégration radioactive.
[modifier] Étude de la fonction N
1. Étudier le sens de variation de la fonction N sur  .
.
2. Étudier la limite de la fonction N en  .
.
3. Dresser le tableau de variation de la fonction N.
[modifier] Exemples
1. Avec t en milliers d'années la constante caractéristique du carbone 14 est λ = 0,121.
Tracer sur la calculatrice la représentation graphique de la fonction f(t) = e − 0,121t sur [0;20[.
2. Utiliser la fonction trace pour déterminer la période de demi-vie,
c'est-à-dire le temps au bout duquel il ne reste que la moitié du carbone.
3. Pour l'uranium-238, λ = 0,154.10 − 6s − 1 et pour l'iode-131, λ = 31625s − 1.
Déterminer leur période de demi-vie à l'aide de la calculatrice.
Exercice : Équations différentielles
Fonction exponentielle/Exercice/Équations différentielles
Une page de Wikiversité.
| Exercice 5 | |||
| Leçon : Fonction exponentielle | |||
|---|---|---|---|
| Chapitre du cours : | Fonction exponentielle | ||
|
Cet exercice est de niveau 12. |
|||
[modifier] Exercice 1
Déterminer l'unique fonction dérivable sur  vérifiant les conditions données.
vérifiant les conditions données.
Puis vérifier que la solution convient dans chaque cas.
1.  et
et  .
.
2.  et
et 
3.  et
et 
[modifier] Exercice 2
Déterminer l'unique fonction dérivable sur  vérifiant les conditions données.
vérifiant les conditions données.
Puis vérifier que la solution convient dans chaque cas.
1.  et
et  .
.
2.  et
et 
3.  et
et 



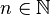 par
par  .
. .
.

 la limite de la suite
la limite de la suite  .
. .
. .
. .
. est dérivable sur
est dérivable sur  .
. est une solution de
est une solution de  a pour dérivée :
a pour dérivée : .
. est constante et comme
est constante et comme  ,
, pour tout x.
pour tout x. pour tout x donc
pour tout x donc  ne s'annule pas.
ne s'annule pas. et
et  ,
, est défine et dérivable sur
est défine et dérivable sur 
 donc
donc  .
. et
et  .
. .
. .
.





 alors il existe a tel que
alors il existe a tel que 
 donc
donc  .
. .
. .
. cela démontre la réciproque d'après
cela démontre la réciproque d'après  .
. (exp ne s'annule pas, voir
(exp ne s'annule pas, voir 
 .
. .
.




 et
et  :
:

 l'hypothèse
l'hypothèse  : «
: «  »
» donc
donc  est vraie
est vraie
 est vraie.
est vraie. .
. s'appelle le nombre de
s'appelle le nombre de 





 . Avec un peu de patience, on finit par trouver que
. Avec un peu de patience, on finit par trouver que  .
. est elle-même :
est elle-même : 
 , définie sur
, définie sur  .
. .
.

 , donc pour tout
, donc pour tout 
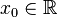 tel que
tel que  ,
, , ce qui est faux car
, ce qui est faux car  , alors f est dérivable et pour tout
, alors f est dérivable et pour tout  .
. car l’exponentielle d’un nombre réel est strictement positive.
car l’exponentielle d’un nombre réel est strictement positive.


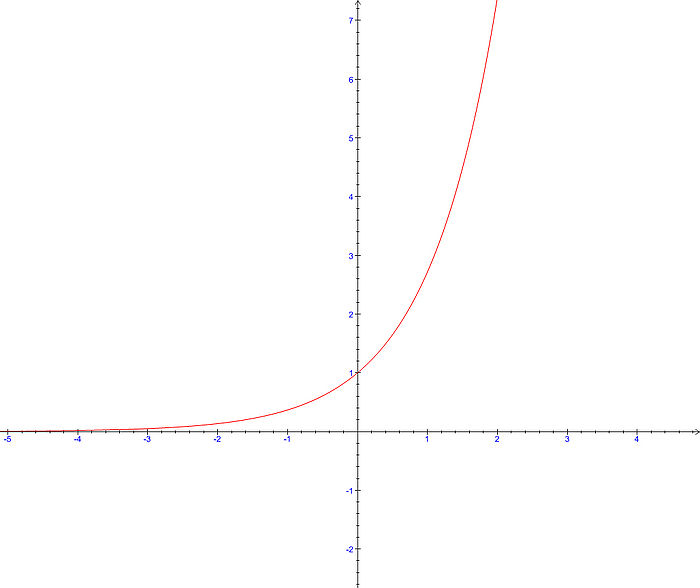
 ,
,
 sur un intervalle I.
sur un intervalle I.














 Donc pour tout
Donc pour tout 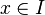































 . On obtient
. On obtient 




 , on peut utiliser la fonction ln pour trouver la solution de (E2) :
, on peut utiliser la fonction ln pour trouver la solution de (E2) :
 .
.
 . Elle admet donc deux racines réelles
. Elle admet donc deux racines réelles  et
et 
 et
et  , qui n'est pas défini
, qui n'est pas défini .
.

 .
.

 d'inconnue x n'admet pas de solution, l'ensemble des solutions de (E5) est réduit à
d'inconnue x n'admet pas de solution, l'ensemble des solutions de (E5) est réduit à
 et
et  donc les quotients n'engendrent pas de restrictions particulières.
donc les quotients n'engendrent pas de restrictions particulières.


 , donc n'admet aucune racine réelle.
, donc n'admet aucune racine réelle.

 .
.

 .
.
 :
:
 donc
donc 

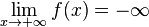


 , définie sur
, définie sur 

 , grandeur négative.
, grandeur négative.





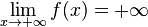


 , définie sur
, définie sur 
 , grandeur positive.
, grandeur positive.

 et
et 
 et
et 


 et
et  et
et 
 et
et 


 et
et 
 et
et 






 , on a pour tout
, on a pour tout 

 et
et 
 et
et 










 et
et  , on a
, on a 
 et
et  , on a
, on a 
 donc
donc 

 . N0 et
. N0 et 
![]0;+ infty[](http://upload.wikimedia.org/math/a/b/e/abe7a92275e0c5644d5bd5c819fa694e.png)