Limites d'une fonction : Limite finie en l'infini
Limites d'une fonction/Limite finie en l'infini
Une page de Wikiversité.
| Chapitre 3 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Chap. préc. : | Limite infinie en un point | ||
| Chap. suiv. : | Limite infinie en l'infini | ||
[modifier] Introduction
Le but du langage des limites est de décrire le comportement des fonctions aux bornes de leur domaine de définition. Une telle borne peut être finie, ce qui donne lieu aux définitions des limites en un point, mais le domaine de définition peut aussi s'étendre jusqu'à l'infini.
|
Exemple 1 |
|
Dans les cas de la fonction inverse, on constate que quand x devient très grand (on dit que x tend vers On note De même, quand x devient très petit (on dit que x tend vers On note |
[modifier] Définition heuristique
|
Définition |
|
Une fonction f tend vers b quand x tend vers en prenant x suffisamment grand, on peut rendre f(x) aussi proche de b que l'on veut. On note alors : |
|
Exemple 2 |

|
|
Exemple 3 |
|
|
Limites d'une fonction : Limite infinie en l'infini
Limites d'une fonction/Limite infinie en l'infini
Une page de Wikiversité.
| Chapitre 4 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Chap. préc. : | Limite finie en l'infini | ||
| Chap. suiv. : | Opérations sur les limites | ||
Sommaire[masquer] |
[modifier] Introduction
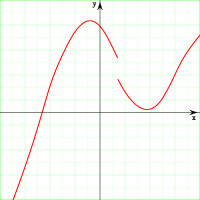
Prenons l'exemple de la fonction carrée, dont la courbe est une parabole.
On constate que quand x devient très grand (on dit que x tend vers plus l'infini), son carré x² devient également très grand (il tend vers plus l'infini également). On dit alors que x² a pour limite + ∞ quand x tend vers + ∞.
On le note  .
.
De la même façon, quand x devient très petit (on dit que x tend vers moins l'infini), son carré x² devient très grand (il tend vers plus l'infini). On dit alors que x² a pour limite + ∞ quand x tend vers - ∞.
On le note  .
.
[modifier] Définition heuristique
|
Définition |
|
Une fonction f tend vers en prenant x suffisamment grand, on peut rendre f(x) aussi grand que l'on veut. On note alors |
[modifier] Exemples
Donner sans démonstration les limites en  des fonctions suivantes :
des fonctions suivantes :
[modifier] Limites des fonctions de référence
|
Théorème |
|
Limites d'une fonction : Limite finie en un point
Limites d'une fonction/Limite finie en un point
Une page de Wikiversité.
| Chapitre 1 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Retour au | Sommaire | ||
| Chap. suiv. : | Limite infinie en un point | ||
Sommaire[masquer] |
[modifier] Limite finie en un réel : définition heuristique
|
Définition |
|
Soit une fonction On dit que
On note alors : |
Remarque :
- On dit aussi : "
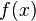 tend vers
tend vers  quand
quand  tend vers
tend vers  ".
".
Exemple : Soit la fonction définie sur  par
par 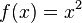 .
.
Conjecturer la limite en 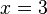 de
de  .
.
Remarque : On pourrait croire que toute fonction  définie en
définie en  a pour limite
a pour limite  en
en  .
.
Mais cela n'est pas toujours le cas. C'est le problème de la continuité.
[modifier] Continuité : définition heuristique et définition formelle
Une fonction f est continue en un point a si on peut atteindre f(a) par la gauche et par la droite en suivant la courbe et « sans lever son crayon ». C'est le cas pour la fonction ci-contre.
En revanche, dans ce cas, la courbe de f présente une « coupure » en x=a qui oblige à « lever le crayon » pour parcourir la courbe. On dit alors que la fonction f est discontinue au point a.
|
Définition |
elle admet en
on dit que |
[modifier] Limite à gauche et à droite
|
Définition |
|
Quand on s'approche de a par la gauche (c'est-à-dire pour x se rapprochant de a tout en restant inférieur à a), la valeur de f(x) s'approche d'une valeur appelée la limite à gauche en x = a. Elle est notée :
|
|
Définition |
|
Quand on s'approche de a par la droite (c'est-à-dire pour x se rapprochant de a tout en restant supérieur à a), la valeur de f(x) s'approche d'une valeur appelée la limite à droite en x = a. Elle est notée :
|
|
Graphe et discontinuité |
|
Une fonction ne peut jamais donner deux valeurs différentes au même endroit. Cela implique que, au niveau d'un point de discontinuité, un seul point appartient effectivement à la courbe :
Cette convention est illustrée sur les graphes des définitions des limites. |
[modifier] Continuité en un point
On peut donner alors une définition plus précise de la continuité :
|
Définition |
|
Une fonction f est continue en x=a si : |
[modifier] Exemple
Soit la fonction :
- Pour a=4, f(a)=8.
- Si x tend vers 4 par la gauche, f(x) va s'approcher de plus en plus de f(4)=8 :
 .
.
- Si x tend vers 4 par la droite, f(x) va s'approcher de plus en plus de f(4)=8 :
 .
.
- Donc f est continue en x=4.
[modifier] Conclusion
La plupart des fonctions usuelles sont continues en tout point de leur domaine de définition. Mais le langage des limites va permettre de parler de celles qui présentent des singularités en certains points, comme la fonction inverse 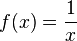 , dont voici la courbe :
, dont voici la courbe :

On constate que la fonction inverse n'est pas continue en x=0, et que non seulement on est obligé de « lever le crayon » pour passer de la branche gauche de la courbe à la branche droite, mais en plus la courbe « part à l'infini ». Ceci nous amène à la notion de limite infinie en un point.
Limites d'une fonction : Limite infinie en un point
Limites d'une fonction/Limite infinie en un point
Une page de Wikiversité.
| Chapitre 2 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Chap. préc. : | Limite finie en un point | ||
| Chap. suiv. : | Limite finie en l'infini | ||
Sommaire[masquer] |
[modifier] Introduction
La plupart des fonctions usuelles sont continues en tout point de leur domaine de définition. Mais le langage des limites va permettre de parler de celles qui présentent des singularités en certains points, comme la fonction inverse 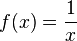 , dont voici la courbe :
, dont voici la courbe :

On constate que la fonction inverse n'est pas continue en x=0, et que non seulement on est obligé de « lever le crayon » pour passer de la branche gauche de la courbe à la branche droite, mais en plus la courbe « part à l'infini ». Ceci nous amène à la notion de limite infinie en un point.
[modifier] Limite infinie en un point
[modifier] Exemple
Dans le cas de la fonction inverse ci-dessus, on constate que quand x tend vers 0 par la droite, son inverse  devient de plus en plus grand. On dit alors qu'il tend vers « plus l'infini », et on note
devient de plus en plus grand. On dit alors qu'il tend vers « plus l'infini », et on note 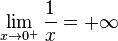
Par contre, quand x tend vers 0 par la gauche, son inverse  devient de plus en plus petit. On dit à ce moment-là qu'il tend vers « moins l'infini », et on note
devient de plus en plus petit. On dit à ce moment-là qu'il tend vers « moins l'infini », et on note 
[modifier] Définition heuristique
|
Définition |
|
On dit qu'une fonction f tend vers plus l'infini en un point a si f(x) devient aussi grand qu'on le veut à condition que x s'approche suffisamment de a. On note : |
|
Définition |
|
On dit qu'une fonction f tend vers moins l'infini en un point a si f(x) devient aussi petit qu'on le veut à condition que x s'approche suffisamment de a. On note : |
On peut également définir des limites infinies à droite ou à gauche d'un point comme on l'a fait avec la fonction inverse.
|
Exemple |
|
Dans le cas de la fonction ci-contre :
|
Limites d'une fonction : Théorèmes sur les limites
Limites d'une fonction/Théorèmes sur les limites
Une page de Wikiversité.
| Chapitre 6 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Chap. préc. : | Opérations sur les limites | ||
| Chap. suiv. : | Limite des polynômes et fractions rationnelles à l'infini | ||
[modifier] Théorèmes de domination
|
Théorème |
|
Soient ƒ et g deux fonctions.
|
En effet, si une fonction donnée prend des valeurs de plus en plus grandes (tendant vers +∞), une autre fonction dont les valeurs seraient encore plus grandes fait de même !
De même, si une fonction donnée prend des valeurs de plus en plus petites (tendant vers -∞), une autre fonction dont les valeurs seraient encore plus petites va tendre également vers -∞.
[modifier] Théorème des gendarmes
|
Théorème |
|
Soit Si Ce théorème est également valable pour une limite en l'infini :
|
Il se comprend facilement qu'une fonction coincée entre deux autres qui ont la même limite est forcée d'avoir elle aussi cette limite par effet « d'entonnoir ».
Le nom de « théorème des gendarmes » reprend cette image. Un voleur attrapé de part et d'autre par deux gendarmes est bien obligé d'aller au même endroit qu'eux. Outre-Manche, ce théorème est parfois appelé « the sandwich theorem ».
|
Exemple |
|
Soit Cette limite est loin d'être facile à trouver si on n'a pas recours au théorème des gendarmes. Il suffit en effet de poser : Comme pour tout Comme de plus |
Limites d'une fonction : Opérations sur les limites
Limites d'une fonction/Opérations sur les limites
Une page de Wikiversité.
| Chapitre 5 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Chap. préc. : | Limite infinie en l'infini | ||
| Chap. suiv. : | Théorèmes sur les limites | ||
Soient f et g deux fonctions définies sur un intervalle contenant a ou dont a est une borne.
« FI » signifie que la forme est indéterminée. Il faut transformer l'écriture de la fonction pour trouver une forme qui permet de calculer la limite.
Sommaire[masquer] |
[modifier] Limite d'une somme

[modifier] Limite d'un produit

Pour déterminer le signe des limites en bleu, on se réfèrera à la règle des signes.
[modifier] Limite d'un quotient

Pour déterminer le signe des limites en bleu, on se réfèrera à la règle des signes.
[modifier] Limite de la composée
Les lettres a, b et c désignent soit des nombres réels, soit  soit
soit  .
.
Soit la fonction composée  définie sur un intervalle I contenant a, ou dont a est une borne.
définie sur un intervalle I contenant a, ou dont a est une borne.
Si  et si
et si  alors
alors 
[modifier] Exemple de la racine carrée

[modifier] Rédaction à tenir
Prenons l'exemple suivant :
|
Exemple |
|
On recherche la limite de la fonction |
|
Méthode pour la limite d'une composée |
|
Pour trouver la limite d'une composée, il faut procéder en plusieurs temps pour procéder proprement.
|
Appliquons cette méthode dans le cas suivant :
|
Exemple |
|
|
On recherche la limite de la fonction
|
Limites d'une fonction : Limite des polynômes et fractions rationnelles à l'infini
Limites d'une fonction/Limite des polynômes et fractions rationnelles à l'infini
Une page de Wikiversité.
| Chapitre 7 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Chap. préc. : | Théorèmes sur les limites | ||
| Chap. suiv. : | Droites asymptotes | ||
Remarque : Les théorèmes qui suivent ne figurent pas au programme de toutes les classes de terminales, voir les fiches d'exercices pour résoudre le problème sans les théorèmes.
Sommaire[masquer] |
[modifier] Cas des polynômes
|
Théorème |
|
La limite d'un polynôme en celle de son terme de plus haut degré. |
[modifier] Exemple
Déterminer les limites aux infinis des fonctions suivantes :
[modifier] Cas des fractions rationnelles
|
Définition |
|
Une fraction rationnelle (ou fonction rationnelle) est un quotient de polynômes. |
|
Théorème |
|
La limite d'une fraction rationnelle (ou fonction rationnelle) en celle du quotient des termes de plus haut degré du numérateur et du dénominateur. |
[modifier] Exemple
Déterminer les limites quand x tend vers  et quand x tend vers
et quand x tend vers  des fractions rationnelles suivantes en précisant la forme indéterminée rencontrée.
des fractions rationnelles suivantes en précisant la forme indéterminée rencontrée.
Limites d'une fonction : Droites asymptotes
Limites d'une fonction/Droites asymptotes
Une page de Wikiversité.
| Chapitre 8 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Chap. préc. : | Limite des polynômes et fractions rationnelles à l'infini | ||
| Chap. suiv. : | Exemple corrigé | ||
Sommaire[masquer] |
[modifier] Définition qualitative
|
Définition |
|
Soit ƒ une fonction dont la courbe représentative dans un repère est notée Une droite |
On peut classer les asymptotes en trois « catégories » :
- Les asymptotes horizontales
- Les asymptotes verticales
- Les asymptotes obliques
[modifier] Asymptote horizontale
Prenons la fonction inverse. On sait que  .
.
Ceci montre que la courbe de la fonction inverse de rapproche de plus en plus de l'axe des abscisses, qui est la droite d'équation  .
.
On dit alors que l'axe des abscisses est asymptote à la courbe de la fonction inverse en +∞.
De même, on a  , donc l'axe des abscisses est asymptote à la courbe de la fonction inverse en -∞.
, donc l'axe des abscisses est asymptote à la courbe de la fonction inverse en -∞.
|
Définition |
|
Soit ƒ une fonction dont la courbe représentative dans un repère est notée
|
[modifier] Asymptote verticale
Prenons à présent la fonction  , dont la courbe
, dont la courbe  est représentée ci-contre.
est représentée ci-contre.
On a  et
et  .
.
On voit alors bien que 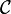 se rapproche de plus en plus de la droite verticale tracée en bleu lorsque x tend vers x₁. La droite en bleu a pour équation
se rapproche de plus en plus de la droite verticale tracée en bleu lorsque x tend vers x₁. La droite en bleu a pour équation 
On dit que 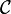 a pour asymptote verticale la droite d'équation
a pour asymptote verticale la droite d'équation  en x₁.
en x₁.
|
Définition |
|
Soit ƒ une fonction dont la courbe représentative dans un repère est notée
|
[modifier] Asymptote oblique
[modifier] Exemple 1
|
Exemple |
|
Soit ƒ la fonction définie sur
|
- 1. Déterminer le comportement de ƒ en

-
- On factorise les termes de plus haut degré et on simplifie :
- Pour tout

-
- Or
 et
et 
- Or
-
- Donc

- Donc
- 2. On note
 . Pour tout
. Pour tout  , donner l'expression de E(x).
, donner l'expression de E(x). -
- Soit


- Soit
- 3. Déterminer la limite de E(x) quand x tend vers plus l’infini.
-
-
- Donc

- Donc
- 4. Sur la calculatrice, tracer la courbe de ƒ et la droite d’équation y = x - 1. Que remarque-t-on ?
[modifier] Théorème général sur les asymptotes obliques
|
Théorème |
|
On pose pour tout
|
Dans l'exemple précédent,  et l'asymptote est ...
et l'asymptote est ...
|
Définition |
|
La quantité |
Dans l'exemple précédent,  .
.
|
Propriété |
|
Si Si |
Dans l'exemple précédent :

[modifier] Exemple 2
|
Exemple |
|
Soit g la fonction définie sur
|
- 1. Déterminer le comportement de g en +∞
On factorise par les termes de plus haut degré et on simplifie :
- Pour tout

- Or,
 et
et 
- Donc

- 2. Trouver a et b tels que pour tout


- 3. On pose pour tout
 . Étudier le signe de E(x) et sa limite quand x tend vers plus l’infini.
. Étudier le signe de E(x) et sa limite quand x tend vers plus l’infini.
- Pour tout

- Or

- Donc

On a les positions relatives :

Limites d'une fonction : Exemple corrigé
Limites d'une fonction/Exemple corrigé
Une page de Wikiversité.
| Chapitre 9 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Chap. préc. : | Droites asymptotes | ||
| Chap. suiv. : | Définitions quantifiées de la notion de limite | ||
|
Exemple |
|
Soit
|
Sommaire[masquer] |
[modifier] Question 1 : Domaine de définition de f
- Soit
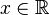

Le domaine de définition de f est  |
[modifier] Question 2 : Étude des limites de f aux bords de son domaine de définition
- Nous allons étudier la limite de f aux infinis, en
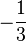 et en 2.
et en 2.
[modifier] Étude en +∞ et en -∞
Soit  On met en facteur les termes de plus haut degré :
On met en facteur les termes de plus haut degré : 


- Donc



- Donc

- Donc
 , c'est-à-dire
, c'est-à-dire
 |
- De même,
 et
et 
Donc  |
[modifier] Étude en 1/3
On pose les deux fonctions suivantes sur  :
:
On a ainsi pour tout 
On a devant nous une limite de la forme  . Il faut donc connaître le signe de f pour savoir si la limite vaut +∞ ou -∞, c'est-à-dire connaître les signes de N et D aux alentours de
. Il faut donc connaître le signe de f pour savoir si la limite vaut +∞ ou -∞, c'est-à-dire connaître les signes de N et D aux alentours de  .
.
 donc N est positive au voisinage de
donc N est positive au voisinage de 
- La fonction D est une fonction polynomiale du second degré. Son tableau de signes est le suivant :
Nous pouvons à présent dire que :
- pour

-
 et
et 
Ainsi  |
- pour
![x in left]-frac{1}{3};2 right[](http://upload.wikimedia.org/math/8/2/c/82c96383c48c526eb5457b9527a99bcb.png)
-
 et
et 
Ainsi,  |
[modifier] Étude en 2
Nous sommes a priori en présence d'une forme indéterminée de type «  ».
».
Il y a cependant un moyen simple de remédier à ce problème. Comme  et
et  et que N et D sont des fonctions polynomiales, il est possible de les factoriser toutes deux par x-2.
et que N et D sont des fonctions polynomiales, il est possible de les factoriser toutes deux par x-2.
Pour trouver la factorisation, il y a plusieurs manières de faire.
- Utilisation des relations coefficients-racines (
 voir le cours sur les équations du second degré)
voir le cours sur les équations du second degré)
-
- On sait qu'une racine de N est 2 et que le produit des racines vaut
 .
. - On en déduit que pour tout

- On sait qu'une racine de N est 2 et que le produit des racines vaut
- Poser α la racine de N que l'on ne connaît pas et déduire α par identification de
 et de
et de 
- Trouver les racines par calcul du discriminant etc, ici DÉCONSEILLÉ par induit beaucoup de calcul pour retomber un résultat que l'on connaît déjà à moitié. Dans ce cas c'est une perte de temps.
La question 1 nous apprend directement que pour tout 
Finalement, soit 
On a fait disparaître la forme indéterminée. Il ne reste plus qu'à écrire la limite :
Finalement : |
Limites d'une fonction : Définitions quantifiées de la notion de limite
Limites d'une fonction/Définitions quantifiées de la notion de limite
Une page de Wikiversité.
| Chapitre 10 | |||
| Leçon : Limites d'une fonction | |||
|---|---|---|---|
| Chap. préc. : | Exemple corrigé | ||
| Chap. suiv. : | Courbes asymptotes | ||
Remarque : Pour une compréhension intuitive de la notion de limite, voyez les premiers chapitres du cours Limites d'une fonction.
Soit  une fonction définie sur un domaine
une fonction définie sur un domaine  à valeurs dans
à valeurs dans  .
.
Sommaire[masquer] |
[modifier] Définitions formalisées
[modifier] Limite finie en un point
|
Définition |
|
|
|
En français, on pourrait dire que  a pour limite
a pour limite  en
en  si, et seulement si, pour un intervalle
si, et seulement si, pour un intervalle  choisi autour de
choisi autour de  aussi petit que l'on veut, il existe un intervalle de valeurs de
aussi petit que l'on veut, il existe un intervalle de valeurs de  autour de
autour de  pour lequel tous les
pour lequel tous les 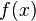 appartiennent à
appartiennent à  .
.
On note alors  ou, de manière plus condensée,
ou, de manière plus condensée, 
[modifier] Limite infinie en un point
|
Définition |
||
|
En français, cela revient à dire que, aussi grand (ou petit) qu'on prenne un réel  , en se rapprochant suffisamment de
, en se rapprochant suffisamment de  , on finit par dépasser la valeur de
, on finit par dépasser la valeur de  .
.  prend ainsi des valeurs infiniment grandes (ou petites) au voisinage de
prend ainsi des valeurs infiniment grandes (ou petites) au voisinage de  .
.
On note :
 ou
ou  si
si  a pour limite
a pour limite  en
en 
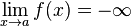 ou
ou  si
si  a pour limite
a pour limite 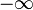 en
en 
[modifier] Limite finie en l'infini
|
Définition |
|
|
|
En français, tout intervalle ouvert contenant  contient aussi toutes les valeurs
contient aussi toutes les valeurs 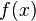 pour
pour  assez grand.
assez grand.
On note  ou
ou 
|
Définition |
|
 a pour limite a pour limite  en en 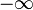 si, et seulement si : si, et seulement si :
|
En français, tout intervalle ouvert contenant  contient aussi toutes les valeurs de
contient aussi toutes les valeurs de  pour
pour  assez petit.
assez petit.
On note  ou
ou 
[modifier] Limite infinie en l'infini
|
Définition |
||
|
En français, cela revient à dire que tout intervalle ![]M ; +infty[](http://upload.wikimedia.org/math/2/0/a/20a36bb3e7685beb082d9952b99d4670.png) avec M > 0 contient toutes les valeurs de
avec M > 0 contient toutes les valeurs de  :
:
- pour
 suffisamment grand si
suffisamment grand si  a pour limite
a pour limite  en
en  . On note alors
. On note alors 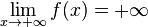 ou
ou 
- pour
 suffisamment petit si
suffisamment petit si  a pour limite
a pour limite  en
en 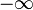 . On note alors
. On note alors  ou
ou 
|
Définition |
||
|
En français, cela revient à dire que tout intervalle ![]-infty;M[](http://upload.wikimedia.org/math/7/9/4/7947fc1ca098471f190464cbd90b8a5b.png) avec M < 0 contient toutes les valeurs de
avec M < 0 contient toutes les valeurs de 
- pour
 suffisamment grand si
suffisamment grand si  a pour limite
a pour limite 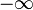 en
en  . On note alors
. On note alors 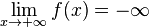 ou
ou 
- pour
 suffisamment petit si
suffisamment petit si  a pour limite
a pour limite 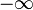 en
en 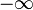 . On note alors
. On note alors 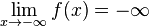 ou
ou 
[modifier] Limite « unilatérale » en un point
|
Définition |
|
|
|
On procède de même pour définir la limite à droite en remplaçant ![]a-delta_{varepsilon};a],](http://upload.wikimedia.org/math/9/4/f/94f77aa32d7c987ed526919c80f2f736.png) par
par  .
.
On note
 ou
ou  pour la première définition
pour la première définition ou
ou  pour la deuxième définition
pour la deuxième définition
[modifier] Limite « épointée » en un point
|
Définition |
|
|
|
On note 
[modifier] Limite « unilatérale épointée » en un point
|
Définition |
|
On note
 pour la première définition
pour la première définition pour la deuxième définition
pour la deuxième définition
|
Définition |
|
On note
 ou
ou  pour la première définition
pour la première définition ou
ou  pour la deuxième définition
pour la deuxième définition
|
Définition |
|
On note
 ou
ou  pour la première définition
pour la première définition ou
ou  pour la deuxième définition
pour la deuxième définition
[modifier] Théorèmes sur les limites
[modifier] Premières propriétés
|
Propriété : Unicité de la limite |
|
Si |
On va maintenant voir comment caractériser une limite de fonction à partir de limite de suite. On ne donne ici la propriété que pour une limite finie en un point, mais elle est transposable aux autres cas :
|
Propriété : Caractérisation séquentielle d'une limite |
|
|
Soient
|
[modifier] Limites et opérations
|
Propriété |
|
Soient
|
Ces propriétés sont aussi valables pour les limites à droite et à gauche, pour le cas p = ±∞, et aussi pour les limites infinies en utilisant les règles suivantes :
- q + ∞ = ∞ pour q ≠ -∞
- q × ∞ = ∞ si q > 0
- q × ∞ = -∞ si q < 0
- q / ∞ = 0 si q ≠ ± ∞.
Remarquons qu'il n'y a pas de règle générale pour le cas q / 0 : cela dépend de la façon dont on s'approche de 0. Certains cas, comme par exemple 0/0, 0×∞ ∞-∞ ou ∞/∞, ne sont pas non plus couverts par ces règles.
[modifier] Formes indéterminées
Il existe certaines formes de limite où il est n'est pas possible de conclure directement en utilisant des opérations sur les limites, ce sont les formes indéterminées (FI) :
- Indétermination de la forme 0/0 quand le résultat obtenu donne 0/0
- Indétermination de la forme ∞/∞ quand le résultat obtenu donne ∞/∞
- Indétermination de la forme ∞ - ∞ quand le résultat obtenu donne ∞ - ∞
- Indétermination de la forme 0 × ∞ qui se ramène aux deux premiers cas en remarquant qu'une multiplication par 0 équivaut à une division par l'infini, ou qu'une multiplication par l'infini équivaut à une division par 0.
Règles opératoires pour lever l'indétermination :
Voici quelques régles opératoires pour lever les FI :
- Fonctions polynomiales et rationnelles :
On a la règle "des monômes de plus haut degré" qui n'est valable qu'en l'infini:
|
Règle |
|
(démonstration à faire) Exemples :
1/ Soit  .Le monôme de plus haut degré est
.Le monôme de plus haut degré est  .
.
Alors 
et de même :  .
.
2/ Soit  .Les monômes de plus hauts degrés sont
.Les monômes de plus hauts degrés sont  et
et  .
.
Alors  .
.
- Factorisation par le terme "le plus fort en l'infini" :
(à faire)
- Régle de L'Hospital :
Du nom du Marquis de L'Hospital, mathématicien français du XVIIème siècle, cette règle permet de simplifier les FI 0/0 ou ∞/∞ : voir Fonctions d'une variable réelle/Dérivabilité).
[modifier] Limite d'une fonction composée
|
Propriété |
|
Soient |
Exemple :Calculer  .
.
On remarque que  :
:
 où
où 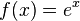 et
et  .
.
Or :
 ;
; (première application de la propriété) ;
(première application de la propriété) ;
donc en appliquant une deuxième fois la propriété :
 |
.
[modifier] Limites et relation d'ordre
Les trois énoncés qui suivent sont valables mutatis mutandis pour  .
.
La propriété qui suit permet de "passer à la limite" dans une inégalité.
|
Propriété |
|
|
Soient
|
Attention ! Cette propriété n'est plus vraie si on remplace les inégalités larges par des inégalités strictes.
Contre-exemple : Il suffit de remarquer que  est à valeurs strictement positives sur
est à valeurs strictement positives sur ![]0;+infty[,](http://upload.wikimedia.org/math/a/c/a/aca50263d6be56405e349875e03d8bad.png) , mais que
, mais que  .
.
On a les deux Théorèmes suivants, qui sont très utiles dans la pratique :
|
Théorème des Gendarmes |
|
Soient f
|




 .
.







 .
.
 est une parabole tournée vers le haut
est une parabole tournée vers le haut est une droite, représentant une fonction croissante
est une droite, représentant une fonction croissante .
.


 et
et  .
.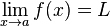
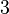 , alors
, alors  tend vers
tend vers 

 .
.









 , alors
, alors 
 , alors
, alors 


 et
et  et
et  , alors
, alors 
 et
et  et
et 
 et
et  et
et 

 . On cherche la limite de g en 0.
. On cherche la limite de g en 0.

 , on a pour tout
, on a pour tout 
 et que
et que  , le théorème des gendarmes permet de montrer que
, le théorème des gendarmes permet de montrer que 
 en
en  et de la fonction racine carrée :
et de la fonction racine carrée : . Appelons-le X.
. Appelons-le X.

 lorsque X tend vers 2.
lorsque X tend vers 2.









 donc
donc 
 donc
donc 
 donc
donc 
 donc
donc 

 donc
donc 
 donc
donc 

 donc
donc 
 donc
donc 








 , donc
, donc 





 , donc
, donc 

 , donc
, donc 


 , donc
, donc 



 , donc
, donc 





 par :
par :
 . Pour tout
. Pour tout 
 et
et 






 , alors la droite d’équation
, alors la droite d’équation  est asymptote à la courbe de ƒ.
est asymptote à la courbe de ƒ.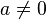 , la droite d’équation
, la droite d’équation 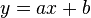 n’est pas horizontale et on parle d’asymptote oblique.
n’est pas horizontale et on parle d’asymptote oblique. est appelée écart vertical algébrique entre la courbe et la droite.
est appelée écart vertical algébrique entre la courbe et la droite. : la courbe est au-dessus de son asymptote.
: la courbe est au-dessus de son asymptote. : la courbe est en dessous de son asymptote.
: la courbe est en dessous de son asymptote.
 par :
par :

 et
et 
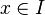

 , c'est-à-dire pour tout
, c'est-à-dire pour tout 




 est asymptote à la courbe
est asymptote à la courbe  de la fonction g.
de la fonction g.

 .
.









 si, et seulement si :
si, et seulement si :![forall varepsilon > 0,existsdelta_{varepsilon} >0,forall xin]a-delta_{varepsilon},a+delta_{varepsilon}[capmathcal D,~|f(x)-l|leqvarepsilon](http://upload.wikimedia.org/math/c/7/e/c7e11afa385e5f65f093439baab43c50.png)

![forall M > 0,existsdelta_{M} >0,forall xin]a-delta_{M},a+delta_{M}[capmathcal D,~f(x)geq M](http://upload.wikimedia.org/math/e/7/d/e7dae1ee9ff3ede6a98f5fba787cd65f.png)
![forall M < 0,existsdelta_{M} >0,forall xin]a-delta_{M},a+delta_{M}[capmathcal D,~f(x)leq M](http://upload.wikimedia.org/math/6/0/9/609ce49f3f9000edb5aeb9cab348c918.png)










![forall varepsilon > 0,existsdelta_{varepsilon} >0,forall xin]a-delta_{varepsilon};a]capmathcal D,~|f(x)-l|leqvarepsilon](http://upload.wikimedia.org/math/9/7/4/974b17117c25894ba959428a672b3837.png)

![forall epsilon >0 ,existsdelta_{varepsilon} >0,forall xin(]a-delta_{varepsilon};a,a[cup]a,a+delta_{varepsilon}[)capmathcal D,~|f(x)-l|leqvarepsilon](http://upload.wikimedia.org/math/b/6/c/b6cf2f1a4b6d1e01fd5e555b20a2849d.png)

![forall epsiloninR^{+*},existsetainR^{+*},forall xin]x_1-eta,x_1[capmathcal D,~|f(x)-y_1|leqepsilon](http://upload.wikimedia.org/math/0/6/1/061d07ccb2709f25b2e9d1037a6dc187.png)
![forall epsiloninR^{+*},existsetainR^{+*},forall xin]x_1,x_1+eta[capmathcal D,~|f(x)-y_2|leqepsilon](http://upload.wikimedia.org/math/7/3/d/73d09637dc63bbe16d58ce5351cc440f.png)

![forall MinR^-,existsetainR^{+*},forall xin]x_1,x_1+eta[capmathcal D,~f(x)leq M](http://upload.wikimedia.org/math/3/f/7/3f7862a73a4d1c24f8a290620e5a933e.png)
![forall MinR^+,existsetainR^{+*},forall xin]x_1-eta,x_1[capmathcal D,~f(x)geq M](http://upload.wikimedia.org/math/3/a/9/3a92e66789ec0a80db623f8a9ff54465.png)
![forall MinR^+,existsetainR^{+*},forall xin]x_1,x_1+eta[capmathcal D,~f(x)geq M](http://upload.wikimedia.org/math/9/f/e/9fe1d671b05ef336de42a4179f7bbace.png)
![forall MinR^-,existsetainR^{+*},forall xin]x_1-eta,x_1[capmathcal D,~f(x)leq M](http://upload.wikimedia.org/math/c/e/f/cef05c54031aad1e44dbf3eaf47ad506.png)
 , alors cette limite est unique.
, alors cette limite est unique. avec
avec  . Alors par définition :
. Alors par définition :

 (l'idée est de prendre
(l'idée est de prendre  "suffisamment petit" pour que les intervalles
"suffisamment petit" pour que les intervalles ![]l-varepsilon ; l + varepsilon[,](http://upload.wikimedia.org/math/6/4/a/64a6245ab2a4485f4e7ef67f1787eb6d.png) et
et ![]l'-varepsilon ; l' + varepsilon[,](http://upload.wikimedia.org/math/c/e/a/cea1e3779e955d62ddcd2406988ab13d.png) ne se croisent pas).
ne se croisent pas). .
.![forall x in ]a-delta^{''}_{varepsilon};a+delta^{''}_{varepsilon}[ , f(x) in ]l-varepsilon ; l + varepsilon[cap ]l'-varepsilon ; l' + varepsilon[,](http://upload.wikimedia.org/math/8/d/4/8d461070f950abfada682a40fa49a298.png) ce qui est absurde, car
ce qui est absurde, car  . On en déduit l'unicité de la limite.
. On en déduit l'unicité de la limite. .
. qui converge vers
qui converge vers  converge vers
converge vers  .
. .
. dans la deuxième définition, on a :
dans la deuxième définition, on a : (la dernière implication vient de la définition de "
(la dernière implication vient de la définition de " deux fonctions définies sur un intervalle
deux fonctions définies sur un intervalle  , et
, et  , alors :
, alors : ;
; ;
; et
et  , alors
, alors  et en particulier
et en particulier  .
.
 , d'après l'inégalité triangulaire. On remarque alors que, si
, d'après l'inégalité triangulaire. On remarque alors que, si  , alors
, alors  . Donc, par définition, on a bien :
. Donc, par définition, on a bien :  .
. .
.![forall x in ]a-delta^{'}_{varepsilon};a+delta^{'}_{varepsilon}[ , |g(x)-l'|<varepsilon Longrightarrow g(x) in ]l'-varepsilon ; l' + varepsilon[ Longrightarrow |g(x)|<max(|l'-varepsilon|,|l'+varepsilon|)=M,](http://upload.wikimedia.org/math/3/e/2/3e2be617929d608ee64c7630c48d0eec.png) donc
donc ![]a-delta^{'}_{varepsilon};a+delta^{'}_{varepsilon}[,](http://upload.wikimedia.org/math/6/c/6/6c6de967fe3d991f625c08b482102b87.png) par
par  .
. et les définitions, si
et les définitions, si  .
. , on obtient le résultat voulu.
, on obtient le résultat voulu. .
. sur l'intervalle
sur l'intervalle  Donc,
Donc, ![forall x in ]a-delta^{'}_{varepsilon};a+delta^{'}_{varepsilon}[ ,left|frac{1}{g}(x) - frac{1}{l'}right| le frac{varepsilon}{l'm} ,](http://upload.wikimedia.org/math/e/3/d/e3dc5871af8b21eee2d14306536dc1f4.png) .
. , on obtient le résultat voulu.
, on obtient le résultat voulu. et
et  , alors
, alors  .
.

 d'où le résultat par définition.
d'où le résultat par définition. ".
".![l le l' iff exist eta > 0 | forall x in ]a-eta ; a+eta[ , f(x) le g(x),](http://upload.wikimedia.org/math/9/7/d/97ddb66bd0510698a8ed71209300b408.png)
 Supposons que
Supposons que  .
. , on obtient que :
, on obtient que :
 .
. On raisonne par contraposée : supposons que
On raisonne par contraposée : supposons que  . Alors d'après ce qu'on vient de démontrer,
. Alors d'après ce qu'on vient de démontrer, ![exist eta > 0 | forall x in ]a-eta ; a+eta[ , f(x) ge g(x),](http://upload.wikimedia.org/math/f/b/5/fb5c3d35c8e72ad6a681f3d3ca26691d.png) , d'où le résultat.
, d'où le résultat. ,
, 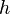 trois fonctions définies "au voisinage de
trois fonctions définies "au voisinage de ![exist eta > 0 | forall x in ]a-eta ; a+eta[ , g(x) le f(x) le h(x),](http://upload.wikimedia.org/math/2/4/4/2440a47315a9439524239604d00d34f2.png) ;
;