Matrice : Introduction générale
Matrice/Introduction générale
Une page de Wikiversité.
| Chapitre 1 | |||
| Leçon : Matrice | |||
|---|---|---|---|
| Retour au | Sommaire | ||
| Chap. suiv. : | Définition (12) | ||
Les matrices sont des objets mathématiques que l'on rencontre très couramment en mathématiques, que ce soit en algèbre linéaire ou en géométrie. Leurs intérêts sont notamment les nombreuses interprétations qu'on peut leur donner, outre le nombre de problèmes qu'elles permettent de résoudre. Cette introduction générale traite des quelques questions « non mathématiques » au sujet des matrices.
Ceux qui souhaitent passer directement à la définition et entrer dans le vif du sujet peuvent sauter ce chapitre introductif.
[modifier] Un peu d'histoire
Si les matrices sous leur formalisme actuel datent du début du XXe siècle, avec notamment l'appui de Heisenberg, l'intérêt pour les « chiffres placés sur une grille » est très ancien. En effet, le problème des « carrés magiques » intriguait déjà les mathématiciens chinois en 650 av. J.-C. et les systèmes d'équations linéaires furent complètement résolues avec les matrices trois siècles plus tard ! La méthode de Cramer (1750) en est l'équivalent moderne.
Le regain formidable d'intérêt pour ces objets au cours du XIXe siècle a motivé des mathématiciens de renom comme Leibniz, Cramer (méthode de Cramer), Gauss (pivot de Gauss), Jordan (réduction de Jordan), Sylvester (inventeur du terme « matrice », matrice de Sylvester), Cayley, Hamilton (mécanique hamiltonienne), Grassmann (formule de Grassmann), Frobenius (théorie des matrices positives), von Neumann...
En 1925, Heisenberg utilise la théorie des matrices pour formuler la mécanique quantique, ancrant définitivement dans l'esprit des mathématicien l'intérêt indéniable de ces objets, et convaincant les physiciens de l'efficacité de son utilisation. Dans les années qui suivent, de nombreux résultats furent découverts, en cryptographie, en calcul, en théorie des graphes, en optique...
Les décompositions de matrices restent des objets de recherche actuels, puisque de tels opérations permettent de séparer le bruit d'une image (décomposition en valeurs singulières), de repérer les caractéristiques d'un code génétique (analyse en composantes principales), d'étudier automatiquement des données statistiques (analyse en composantes indépendantes), le langage humaine (analyse sémantique latente)...
La généralisation de la théorie des matrices, appelée théorie des « tenseurs », est au cœur de la formulation actuelle de la théorie de la relativité générale. Ces objets et leurs extensions sont donc inévitables en physique classique (mécanique hamiltonienne), quantique et relativiste !
[modifier] Interprétations
Ce qui fait la force des matrices, c'est qu'elles sont plus que de simples tableaux de chiffres. Non pas que, nous le verrons, il puisse s'agir d'autres choses que des chiffres, mais elles constituent de véritables objets à part entière. On peut les interpréter de différentes manières, selon le contexte — et certains résultats apparaissent « à l'œil ».
On peut en effet voir les matrices comme des transformations (transformations linéaires) : rotations, déformations... ou bien comme des opérateurs (opérateurs linéaires), comme des données statistiques corrélées... Il en va de même pour leurs opérations : le produit matriciel, l'inversion... tout cela peut être compris différemment selon le contexte.
Il y a de nombreux liens entre les matrices et d'autres domaines des mathématiques, les propriétés des premières pouvant être vues comme d'autres résultats dans les seconds.
La théorie des matrices actuelle étend ses résultats à la théorie des graphes, à l'algèbre, à la combinatoire et aux statistiques, soit autant de visions possibles.
Matrice : Définition
Matrice/Définition
Une page de Wikiversité.
| Chapitre 2 | |||
| Leçon : Matrice | |||
|---|---|---|---|
| Chap. préc. : | Introduction générale | ||
| Chap. suiv. : | Addition et soustraction (12) | ||
Ce chapitre introduit la notion de matrice, et d'ensemble de matrice. Nous précisons les notations usuelles et définissons les termes.
Sommaire[masquer] |
[modifier] Notations générales
|
Notations générales |
|
Soit De manière similaire, si pour la désigner, m et n étant deux nombres entiers positifs et non-nuls. On notera par :
respectivement le corps des nombres réels celui des nombres complexes. La notation On notera en caractères gras les matrices et les vecteurs : Les lettres désignant des nombres seront en minuscules italiques : Le produit sera noté par un point ( |
[modifier] Définition
|
Définitions |
|
Une matrice est la donnée une famille Les nombres m et n sont appelés dimensions de la matrice. On dit qu'une matrice est de taille m × n (lire « m fois n »). Les éléments |
Tout de suite, introduisons la notation usuelle des matrices :
[modifier] Remarques
Lorsqu'on est amené à « lire » une matrice, on énonce ses coefficients de haut en bas, de gauche à droite, c'est-à-dire en respectant l'ordre de la famille : i, puis j.
Il existe une notation alternative des matrices, privilégiée dans la littérature anglo-saxonne mais que nous n'emploierons pas dans le cadre de cette leçon :
Cette notation est parfois utile quand on doit exprimer des grandes expressions où il devient maladroit d'écrire les parenthèses.
[modifier] Exemples
|
Exemples de matrices |
|
Les objets suivants sont des matrices : |
Matrice : Addition et soustraction
Matrice/Addition et soustraction
Une page de Wikiversité.
| Chapitre 2 | |||
| Leçon : Matrice | |||
|---|---|---|---|
| Chap. préc. : | Définition | ||
| Chap. suiv. : | Produit matriciel (12) | ||
Tout comme on peut additionner des nombres ou des vecteurs, il est possible d'effectuer l'addition de deux matrices. Il s'agit d'une opération élémentaire et assez intuitive.
Sommaire[masquer] |
[modifier] Additionner et soustraire
[modifier] Somme de deux matrices
|
Somme de deux matrices |
||
|
Soit A et B deux matrices de même taille sur le même anneau. Alors il est possible de les additionner. Leur somme est une matrice A+B de même taille que A et B :
|
|
Remarque |
|
De manière évidente, si A, B et C sont trois matrices de même taille, alors : On parle d’associativité pour l'addition. |
[modifier] Différence de deux matrices
|
Différence de deux matrices |
|
De manière similaire, on peut soustraire deux matrices A et B lorsqu'elle sont de même taille : |
[modifier] La matrice nulle
|
Matrice nulle |
|
Il existe une matrice telle que l'on peut l'ajouter ou la soustraire à toute autre matrice A sans changer cette dernière. Elle est appelée matrice nulle et notée 0 ou avec « 0 » l'élément neutre pour l'addition dans l'anneau A — si |
|
Structure de |
|
L'ensemble |
[modifier] Exemples
|
Exemples |
|
Un exemple d'addition de deux matrices : Un exemple de soustraction de deux matrices : |
[modifier] Remarques
- Il existe une autre « somme » envisageable pour les matrices, appelée « somme directe ». Elle a un sens dans la théorie des espaces vectoriels, et nous ne l'aborderons pas ici.
- Si les matrices considérées n'ont qu'une seule ligne et une seule colonne (ce sont des nombres), on retrouve ce que l'on sait des nombres concernant leur addition, leur soustraction et le zéro.
- Si les matrices considérées n'ont qu'une colonne (ce sont des vecteurs), on retrouve ce que l'on sait des vecteurs concernant l'addition, la soustraction et le vecteur nul.
Les matrices peuvent donc être vues comme une « généralisation » des vecteurs.
Matrice : Produit matriciel
Matrice/Produit matriciel
Une page de Wikiversité.
| Chapitre 4 | |||
| Leçon : Matrice | |||
|---|---|---|---|
| Chap. préc. : | Addition et soustraction | ||
| Chap. suiv. : | Déterminant (12) | ||
Nous allons introduire dans ce chapitre la notion de produit matriciel. Cette notion n'est malheureusement ni intuitive ni immédiate : il faudra prendre soin de bien la maîtriser.
Sommaire[masquer] |
[modifier] Multiplication par un scalaire
Avant de se lancer dans les choses difficiles, rappelons qu'il est toujours possible de multiplier une matrice A par un nombre réel ou complexe x. De manière évidente :
est la matrice dont les coefficients sont de A multipliés par x.
|
Exemple : multiplication par un scalaire |
|
|
[modifier] Produit de matrices
|
Définition formelle |
|
Soient |
|
Quand est-ce que 2 matrices peuvent être mises en produit ? |
|
Le produit matriciel de 2 matrices A et B n'est réalisable que si A a le même nombre de colonne que B a de lignes. |
|
Définition « plus claire » |
|
Évidemment, la formule du produit matriciel est généralement inutilisable en exercice, même si elle peut être utile pour les démonstrations. Tentons de la clarifier. Pour calculer le premier coefficient de la première ligne :
Pour calculer les autres coefficients, on procède de même avec les autres colonnes de B (on aura ainsi tous les coefficients de la première ligne de A · B), puis avec la seconde ligne de A etc. Il est coutume de poser un produit matriciel comme sur le dessin ci-contre : la première à gauche, la seconde au dessus. Le résultat est la matrice au centre. |
|
Remarque |
||
Comme on peut le voir, l'ordre des matrices dans le produit a une importance : en effet, le produit n'est défini que si le nombre de colonnes de la première égale le nombre de lignes de la seconde. Dans notre exemple, A · B existe, mais B · A n'existe pas... Dans le cas général, on a même |
[modifier] Exemples
Cette notion mérite bien quelques exemples qui permettront aussi d'y voir plus clair. Le lecteur est invité à les reproduire pour vérifier qu'il a bien compris le produit matriciel, à titre d'exercice.
|
Produit matriciel (détaillé) |
|
|
|
Produit matriciel (détaillé) |
||
|
|
Plus simple produit vectoriel |
|
Le produit suivant donne : Alors que : |
[modifier] Matrice identité
Pour les matrices carrées, il existe une matrice qui, multipliée à toute autre, ne la modifie pas.
|
Matrice identité |
|
On appelle matrice identité l'unique matrice In de On montre facilement qu'elle s'écrit : |
|
Exemple : matrice I₂ |
|
La matrice I₂ s'écrit : |
[modifier] Remarques
Il existe d'autres « produits » de matrices, comme le produit de Hadamard ou le produit de Kronecker. Nous ne les aborderons pas dans le cadre de cette leçon. Le produit tensoriel, en revanche, sera l'objet d'un chapitre.
Le produit d'un vecteur ligne par un vecteur colonne est un nombre. Ce nombre est le produit scalaire des deux vecteurs.
L'efficacité algorithmique du produit matriciel est toujours l'objet de recherches actuelles. L'algorithme manuel présenté dans ce chapitre possède une complexité en O(n³). L'algorithme de Coppersmith-Winograd (1990) possède une complexité en O(n2,376), mais n'est réellement efficace que pour de très grosses matrices.
Matrice : Déterminant
Matrice/Déterminant
Une page de Wikiversité.
| Chapitre 5 | |||
| Leçon : Matrice | |||
|---|---|---|---|
| Chap. préc. : | Produit matriciel | ||
| Chap. suiv. : | Trace | ||
Soit une matrice A=(aij) carrée d’ordre n à coefficients réels. Les vecteurs colonnes de la matrice peuvent être identifiés à des éléments de l'espace vectoriel  . Ce dernier est muni d'une base canonique.
. Ce dernier est muni d'une base canonique.
Il est alors possible de définir le déterminant de la matrice A comme le déterminant du système de ses vecteurs colonnes relativement à la base canonique. Il est noté det(A) puisqu'il n'y a pas d'ambiguïté sur la base de référence.
Par définition même, le déterminant dépend de façon linéaire de chaque colonne, et est nul lorsque deux colonnes sont égales. Le déterminant de la matrice identité vaut un. Enfin il vérifie la formule de Leibniz
Ce déterminant se note fréquemment avec des barres verticales :
La présentation matricielle apporte une propriété essentielle : une matrice a même déterminant que sa transposée.
Ce qui signifie que le déterminant de A se voit aussi comme le déterminant du système des vecteurs lignes, relativement à la base canonique.
Matrice : Trace
Matrice/Trace
Une page de Wikiversité.
| Chapitre 6 | |||
| Leçon : Matrice | |||
|---|---|---|---|
| Chap. préc. : | Déterminant | ||
| Chap. suiv. : | Inverse (12) | ||
Dans tous le chapitre, on ne traitera que des matrices carrées. Nous allons introduire la trace, qui constitue un outil de base d'étude des matrices.
Sommaire[masquer] |
[modifier] Définition
|
Trace d'une matrice |
|
Soit A une matrice carrée n × n. La trace de A est la somme des éléments diagonaux de A, elle est notée : Il s'agit d'une forme linéaire sur |
|
Exemples |
|
Soit la matrice : Alors sa trace est : La trace de In est n. La trace de la matrice nulle est 0. |
| Il s'agit bien de la diagonale qui va du coin en haut à gauche au coin en bas à droite. |
[modifier] Propriétés
|
Propriétés |
|
Soient A et B deux matrices carrées de même taille, si a est un nombre, alors : |
|
Démonstration |
|
Les deux premières propriétés sont immédiates. La dernière n'est pas beaucoup plus subtile : |
|
La trace est un invariant de similitude |
|
Soit A et B deux matrices carrées, telles qu'il existe une matrice P inversible vérifiant : c'est-à-dire que A est semblable à B, alors : |
|
Démonstration |
|
|
|
Propriété |
|
Le fait que la trace soit identique pour deux matrices semblables signifie que la trace d'une matrice est une propriété intrinsèque de la matrice, peu importe la base dans laquelle on l'exprime. Elle est donc l' « empreinte », la « trace » d'une matrice. Réciproquement, on montre que toute forme linéaire invariante par similitude est proportionnelle à la trace. |
[modifier] Produit scalaire
L'utilisation de la trace permet de définir le produit scalaire canonique de  :
:
|
Produit scalaire canonique des matrices carrées |
|
On définit le produit scalaire canonique et on note |
|
Exemple |
|
Soient les matrices : Alors leur produit scalaire vaut : |
Ce produit scalaire induit une norme (la norme de Frobenius), mais cela fera l'objet d'un autre chapitre.
[modifier] Remarques
Une autre notation pour la trace est Tr.
En théorie des graphes, on peut associer à tout graphe une matrice, dite matrice d'adjacence. Si le graphe ne contient aucun sommet connecté à lui-même, alors la trace de cette matrice est nulle.
Matrice : Inverse
Matrice/Inverse
Une page de Wikiversité.
| Chapitre 7 | |||
| Leçon : Matrice | |||
|---|---|---|---|
| Chap. préc. : | Trace | ||
| Chap. suiv. : | Matrices particulières | ||
Sommaire[masquer] |
[modifier] Introduction
Après avoir vu qu'il était possible de multiplier des matrices entre elles, on peut naturellement se demander s'il est possible de « diviser » par des matrices. Une telle chose n'a pas de sens rigoureux mathématiquement, et amène à la notion d'inverse, développée dans ce chapitre.
[modifier] Exemple motivant
Soit une équation simple impliquant des nombres réels :
On suppose a et b non-nuls. Alors la solution existe, elle est unique, et il s'agit de :
On cherche à trouver quelque chose d'équivalent pour les matrices, qui permettrait de résoudre les équations matricielles de même type :
[modifier] Définition
|
Inverse d'une matrice |
|
Soit M une matrice carrée de taille n × n. Lorsqu'elle existe, on appelle inverse de M, et on note M⁻¹ l'unique matrice carrée de taille n × n telle que : |
On peut remarquer, d'après les propriétés du déterminant vues dans un précédent chapitre, que :
Cette relation ne peut pas être vérifiée si le déterminant de M est nul. Le théorème suivant renforce cette constatation :
|
Existence et unicité de l'inverse |
|
Soit une matrice carrée M. Alors M admet un unique inverse si et seulement si : Alors, on a : Une matrice dont le déterminant n'est pas nul est dite matrice inversible. |
[modifier] Propriétés de l'inverse
|
Propriétés de l'inverse d'une matrice |
|
| Attention ! Cette dernière règle est souvent négligée et source d'erreurs ! |
[modifier] Ensemble des matrices inversibles
|
Propriété |
|
Pour toutes matrices inversibles A et B de même taille n × n, on a : Cela fait que l'ensemble des matrices inversibles de taille n × n possède une structure de groupe multiplicatif. On l'appelle groupe général linéaire ou groupe linéaire et on le note : |
Il est à noter que les matrices sont « presque toutes » inversibles (on peut donner un sens rigoureux à cela). Si on prend une matrice « au hasard », la probabilité qu'elle soit non-inversible (c'est-à-dire de déterminant exactement 0) est nulle. En physique notamment, où l'on est parfois amené à inverser des matrices de mesures, on ne se pose même pas la question !
Celà n'est vrai que lorsque l'on travaille dans R (les réels). Lorsque l'on travaille dans des ensembles plus complexes (comme par exemple Z/26Z, très courant en cryptographie), l'inversibilité d'une matrice est loin d'aller de soi.
[modifier] Calcul de l'inverse
Calculer l'inverse d'une matrice est une tâche ardue à la main dès lors qu'on aborde les matrices 3 × 3, et la difficulté croît avec la taille.
[modifier] Cas des matrices 2 × 2
|
Inverse d'une matrice 2 × 2 |
|
Un cas très simple (et à mémoriser) est celui des matrices de taille 2 × 2, dont l'inverse est très facile à calculer. Soit la matrice : Alors :
|
|
Démonstration |
|
La démonstration est immédiate : il suffit de faire le produit. Comme l'inverse est unique, ce calcul est suffisant. |
|
Exemple |
|
Soit la matrice A définie par : Alors : |
[modifier] Cas général
Le moyen le plus simple est d'utiliser la méthode dite du pivot de Gauss.
|
Exemple |
||
|
Soit la matrice A définie par : On met en face la matrice que l'on cherche a inverser et la matrice identité : on a donc : On applique alors le pivot de Gauss en ligne Sur les deux matrices symétriquement jusqu'à obtenir la matrice identité a la place de A et l'on obtient la matrice A-1 a la place de la matrice identité:
|
[modifier] Inversion par blocs
[modifier] Interprétations
Dire qu'une matrice A est inversible équivaut à chacune des propositions suivantes :
- A est équivalente à la matrice unité ;
- le déterminant de A est non nul : det (A) ≠ 0,
- le rang de A est égal à n ;
- les colonnes de A, considérées comme des vecteurs de
 forment une base de
forment une base de  ;
;



 une famille d'objets. On utilisera la notation
une famille d'objets. On utilisera la notation ![a_{i in left[![1, n ]!right]},](http://upload.wikimedia.org/math/c/d/c/cdcb0163b42691dbe9094652c0efa763.png) pour désigner cette famille, n étant un entier positif non-nul.
pour désigner cette famille, n étant un entier positif non-nul. est une famille d'objets, on utilisera la notation :
est une famille d'objets, on utilisera la notation :![a_{(i,j) in left[![1, n ]!right] times left[![1, m ]!right]},](http://upload.wikimedia.org/math/8/5/4/8542c28ab40f79bb83387f62048834fc.png)
 et
et 
 désignera indépendamment l'un ou l'autre des deux corps précédents.
désignera indépendamment l'un ou l'autre des deux corps précédents.

 ) pour ne pas le confondre avec le produit cartésien (
) pour ne pas le confondre avec le produit cartésien ( ).
).![a_{i,j in left[[1, n ]right] times left[[1, m ]right]},](http://upload.wikimedia.org/math/7/0/9/709db1f2ac2f1c5de7c12fd0a3c4e781.png) , dont les éléments appartiennent à un anneau commutatif (c'est-à-dire, pour résumer, qu'on sait les additionner et les multiplier entre eux).
, dont les éléments appartiennent à un anneau commutatif (c'est-à-dire, pour résumer, qu'on sait les additionner et les multiplier entre eux).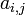 sont appelés coefficients de la matrice.
sont appelés coefficients de la matrice.![mathbf A = a_{i,j in left[[1, n ]right] times left[[1, m ]right]},](http://upload.wikimedia.org/math/5/1/4/514723877d7e4bf3687cde433f444e68.png) est notée de la manière suivante :
est notée de la manière suivante :
 , ou A est l'ensemble d'où sont issus les coefficients. Puisque nous serons amenés à traiter le cas important des matrices carrées sur le corps des réels ou des complexes, on note l'ensemble de ces matrices :
, ou A est l'ensemble d'où sont issus les coefficients. Puisque nous serons amenés à traiter le cas important des matrices carrées sur le corps des réels ou des complexes, on note l'ensemble de ces matrices :










 . De manière évidente :
. De manière évidente :
 ou
ou  c'est simplement le zéro habituel.
c'est simplement le zéro habituel.




![mathbf A = a_{i,j in left[[1, m]right] times left[[1, n]right]} in mathfrak M_{m,n}](http://upload.wikimedia.org/math/d/0/f/d0fab18d468a2e77fdd30b288c165c5a.png) et
et ![mathbf B = b_{i,j in left[[1, n]right] times left[[1, p]right]} in mathfrak M_{n,p}](http://upload.wikimedia.org/math/9/3/d/93db61d98bddf3088fe3880526105540.png) deux matrices. On définit le produit de A par B comme la matrice m × p suivante :
deux matrices. On définit le produit de A par B comme la matrice m × p suivante :![mathbf A cdot mathbf B = left( sum_{k=1}^{n} a_{i,k} cdot b_{k,j} right)_{i,j in left[[1, m]right] times left[[1, p]right]} = begin{pmatrix}
sum_{k=1}^{n} a_{1,k}b_{k,1} & sum_{k=1}^{n} a_{1,k}b_{k,2} & cdots & sum_{k=1}^{n} a_{1,k}b_{k,p}
sum_{k=1}^{n} a_{2,k}b_{k,1} & sum_{k=1}^{n} a_{2,k}b_{k,2} & cdots & sum_{k=1}^{n} a_{2,k}b_{k,p}
vdots & vdots & ddots & vdots
sum_{k=1}^{n} a_{m,k}b_{k,1} & sum_{k=1}^{n} a_{m,k}b_{k,2} & cdots & sum_{k=1}^{n} a_{m,k}b_{k,p} end{pmatrix}](http://upload.wikimedia.org/math/4/b/0/4b0c16e77b51a899b3f7bc1f7107ee6f.png)

 ...
...











 , on peut donc effectuer ce changement d'indice et ainsi
, on peut donc effectuer ce changement d'indice et ainsi










 l'application bilinéaire :
l'application bilinéaire :

















 .
.

 & :
& : 
 & :
& : 
 & :
& : 