Nombre complexe : Introduction de i
Nombre complexe/Introduction de i
Une page de Wikiversité.
| Chapitre 1 | |||
| Leçon : Nombre complexe | |||
|---|---|---|---|
| Retour au | Utilité des nombres complexes | ||
| Chap. suiv. : | Opérations sous forme algébrique | ||
Sommaire[masquer] |
[modifier] Le nombre i
|
Définition |
|
On définit le nombre |
- Le symbole
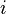 signifie « imaginaire ». En effet, comme le carré d'un nombre réel est toujours positif, ce nombre ne peut pas être un nombre réel ;
signifie « imaginaire ». En effet, comme le carré d'un nombre réel est toujours positif, ce nombre ne peut pas être un nombre réel ; - par convention, i n'est jamais écrit sous la racine carrée ;
- très souvent, il est placé au numérateur d'une fraction ;
- la place de i n'est pas obligatoirement devant ou derrière l'expression, mais nous plaçons i devant le radical comme nous le faisons pour des inconnues quelconques ;
- le plus souvent (uniquement parce que la prononciation est plus simple ainsi), nous plaçons i après les nombres mais avant les inconnues.
[modifier] Forme algébrique d'un nombre complexe
|
Définition |
|
Les nombres qui s'écrivent Cette écriture des nombres complexes est nommée algébrique (ou parfois cartésienne). |
[modifier] La partie réelle et la partie imaginaire
|
Définition |
|
Pour
|
|
Propriété |
|
On utilise aussi la notation suivante pour représenter les 2 parties d'un nombre complexe :
|
|
Exemple : z = − 1 + 2i |
|
[modifier] Les nombres réels et les imaginaires purs
|
Définition |
|
Pour
|
|
Exemple |
|
|
[modifier] Note
Là où nous utilisions plus volontiers la lettre  pour désigner des réels, nous utilisons plutôt la notation
pour désigner des réels, nous utilisons plutôt la notation  pour les nombres complexes.
pour les nombres complexes.
Nombre complexe : Représentation géométrique
Nombre complexe/Représentation géométrique
Une page de Wikiversité.
| Chapitre 4 | |||
| Leçon : Nombre complexe | |||
|---|---|---|---|
| Chap. préc. : | Opérations sous forme algébrique | ||
| Chap. suiv. : | Conjugué d'un nombre complexe | ||
Pour comprendre les nombres complexes, il faut pouvoir les visualiser dans un espace que nous connaissons au préalable. Le problème est que ces nombres complexes n'ont pas de représentation physique, nous ne pouvons par exemple les ordonner sur une règle, chose facile à faire pour les nombres réels.
Néanmoins, le plan complexe (appelé aussi plan d'Argand ou plan d'Argand-Cauchy) permet de résoudre ce problème.
Sommaire[masquer] |
[modifier] Affixe d'un point du plan
|
Définition |
|
Dans le plan muni d'un repère orthonormé, on associe au point M de coordonnées (a;b) son affixe, le nombre complexe z=a+ib. M est appelé image de |
- On a ainsi une correspondance entre les nombres complexes et les points du plan, qui permet de représenter géométriquement les nombres complexes.
- Dans le graphique ci-dessous, on assimile les nombres complexes à leurs images :
- l'image M(4;4) et son affixe le nombre complexe z = 4 + 4i
- Plus généralement :
- La partie réelle du nombre complexe est l'abscisse de son image
- Sa partie imaginaire est l'ordonnée de son image
Graphiquement, on obtient :

[modifier] Affixe d'un vecteur
|
Définition |
|
Au vecteur |
[modifier] Propriétés de l'affixe
[modifier] Affixe d'un vecteur
|
Propriété |
|
L'affixe d'un vecteur |
|
Exemple |
|
Dans la figure ci-contre, on a les points A(1;1) et B(4;3). L'affixe d'un vecteur En effet les coordonnées de |
[modifier] Affixe d'un milieu
|
Propriété |
|
L'affixe du milieu |
|
Exemple |
|
Toujours dans la figure ci-contre dont les points A et B ont pour coordonnées: A(1;1) et B(4;3).
Les coordonnées de |
[modifier] Parallélisme et alignement
|
Propriété |
|
Deux droites |
[modifier] Exemple
Un exemple est le bienvenu.
Nombre complexe : Opérations sous forme algébrique
Nombre complexe/Opérations sous forme algébrique
Une page de Wikiversité.
| Chapitre 2 | |||
| Leçon : Nombre complexe | |||
|---|---|---|---|
| Chap. préc. : | Introduction de i | ||
| Chap. suiv. : | Représentation géométrique | ||
Les nombres complexes respectent les règles valables pour les quatre opérations sur les nombres réels (addition, soustraction, multiplication et division).
Sommaire[masquer] |
[modifier] Égalité de deux nombres complexes
|
Propriété |
|
Deux nombres complexes sont égaux si et seulement si leurs parties réelles sont égales et leurs parties imaginaires sont égales. Ceci signifie, pour deux nombres complexes
|
[modifier] Addition
|
Propriété |
|
Pour additionner deux nombres complexes sous forme algébrique, on additionne :
|
[modifier] Exemples
|
Addition de deux nombres complexes |
|
Soient On a : |
La soustraction se fait de la même manière :
|
Soustraction de deux nombres complexes |
|
Soient On a : |
[modifier] Multiplication
|
Propriété |
|
La multiplication de deux nombres complexes se fait en appliquant la règle de distributivité de la multiplication sur l'addition. Pour
|
- Cette formule n'a pas à être retenue par cœur, il vaut mieux refaire le calcul dans chaque exemple.
[modifier] Exemples
|
Multiplication de deux nombres complexes |
|
Soient
|
[modifier] Puissances de i
La propriété de i que nous allons voir ici est assez simple mais il ne faut pas l'oublier pour les calculs par la suite.
Sachant que  , calculer les autres puissances de i et représenter les images de i dans le plan complexe.
, calculer les autres puissances de i et représenter les images de i dans le plan complexe.
...
avec n = 4q+r : q étant la partie entière du quotient n/4 et r le reste de ce quotient.
Si n est un entier, r ne peut avoir que quatre valeurs différentes ( 0, 1, 2 et 3), et ainsi i ⁿ ne peut avoir que quatre valeurs :
- +1 pour r = 0,
- + i pour r = 1,
- -1 pour r = 2,
- - i pour r = 3.
[modifier] Division
|
Division de deux nombres complexes |
|
Soient On a On est ici dans une impasse car il faudrait remonter i au numérateur |
La division de deux nombres complexes sous forme algébrique utilise la notion de complexe conjugué, qui fait l'objet d'un chapitre spécifique.
[modifier] Exemple de manipulation des complexes : résolution des équations du second degré
Les nombres complexes ont été inventés car ils permettent (entre autres) de résoudre toutes les équations du second degré, même celles qui ont un discriminant négatif.
|
Exemple |
|
L'équation Elle n'a donc pas de solutions réelles. En revanche, en passant dans l'ensemble des nombres complexes, nous pouvons écrire que : Nous pouvons alors résoudre l'équation avec les formules habituelles :
L'équation du second degré |

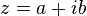 (avec a et b réels) forment l'ensemble
(avec a et b réels) forment l'ensemble 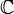 des nombres complexes.
des nombres complexes. voulant dire la partie réelle de z et
voulant dire la partie réelle de z et  voulant dire la partie imaginaire de z, ce qui nous donne :
voulant dire la partie imaginaire de z, ce qui nous donne :

 ,
,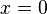 alors
alors  alors
alors  est un imaginaire pur
est un imaginaire pur est un réel
est un réel de coordonnées
de coordonnées  , on associe son affixe
, on associe son affixe 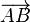 est :
est :  .
.


 d'un segment
d'un segment ![[AB],](http://upload.wikimedia.org/math/c/6/2/c62ec6ac582c054ab2af9aa78971de1b.png) est
est  .
. , l'affixe du milieu du vecteur
, l'affixe du milieu du vecteur 

 et
et  sont parallèles si et seulement si les vecteurs
sont parallèles si et seulement si les vecteurs 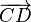 sont colinéaires, c'est-à-dire si et seulement s'il existe un nombre réel
sont colinéaires, c'est-à-dire si et seulement s'il existe un nombre réel  tel que
tel que  , c'est-à-dire qu'il existe un
, c'est-à-dire qu'il existe un  avec
avec  .
. et
et  ,
, si et seulement si
si et seulement si 

 et
et  .
.












 a pour discriminant :
a pour discriminant :



 admet donc
admet donc  et
et  comme solutions complexes.
comme solutions complexes.