Introduction aux suites numériques : Suites arithmétiques
Introduction aux suites numériques/Suites arithmétiques
Une page de Wikiversité.
| Chapitre 2 | |||
| Leçon : Introduction aux suites numériques | |||
|---|---|---|---|
| Chap. préc. : | Définitions | ||
| Chap. suiv. : | Suites géométriques | ||
Sommaire[masquer] |
[modifier] Définition par récurrence
|
Définition |
|
Une suite est arithmétique quand on ajoute toujours le même nombre pour passer d'un terme au suivant. Une suite arithmétique est donc définie par :
Le nombre r qui permet de passer d'un terme au suivant s'appelle la raison de la suite (un). |
[modifier] Exercices d'application
Parmi les suites ci-dessous, lesquelles sont arithmétiques ? Quelle est alors leur raison ?

- 2, 5, 7, 12, 19, 31, 50, 81, ...
- 0, 5, 10, 15, 20, 25, 30, ...
- 7, 14, 28, 56, 112, 224, 448, ...
- 5, 3, 1, -1, -3, -5, -7, -9, -11, -13, ...
[modifier] Terme général d'une suite arithmétique
Pour arriver à un, il faut ajouter n fois la raison r au premier terme u₀
|
Théorème |
|
Le terme général d'une suite arithmétique (un) est donné par la formule :  |
[modifier] Utilisation du terme général
- Soit
 une suite arithmétique telle que
une suite arithmétique telle que  et
et  . Calculer
. Calculer  .
. - Soit
 une suite arithmétique telle que
une suite arithmétique telle que  et
et  . Calculer
. Calculer  .
. - Soit
 une suite arithmétique telle que
une suite arithmétique telle que  et
et  . Calculer
. Calculer  .
. - Soit
 une suite arithmétique telle que
une suite arithmétique telle que  et
et  . Calculer
. Calculer  .
. - Soit
 une suite arithmétique telle que
une suite arithmétique telle que  et
et  . Calculer
. Calculer 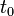 et
et  .
.
[modifier] Somme des termes d'une suite arithmétique
[modifier] Somme des premiers entiers
Comment calculer simplement ?

Il suffit d'utiliser la formule :

On trouve donc :

[modifier] Généralisation
|
Théorème |
|
La somme des (n+1) premiers termes d'une suite arithmétique est donnée par la formule :  |
La somme des termes d'une progression arithmétique est égale à la demi-somme des termes extrêmes multipliée par le nombre des termes de la suite.
[modifier] Calculs de sommes
En utilisant la formule, calculer :
[modifier] Sens de variation
|
Théorème |
|
Une suite arithmétique de raison r est :
|
[modifier] Représentation graphique et lien avec les fonctions affines
Pour une suite arithmétique de premier terme u₀ et de raison r, l'expression du terme général montre que :
si on définit la fonction affine  , alors un = f(n).
, alors un = f(n).
|
Théorème |
|
Pour une suite arithmétique de premier terme u₀ et de raison r, si on place n en abscisse et un en ordonnée, les points correspondants sont alignés sur la droite représentative de la fonction affine :  |
Si un = a + bn , alors (un) est une suite arithmétique de raison b et de premier terme a.
[modifier] Graphiques
- Placer dans un repère orthogonal les 10 premiers termes de la suite arithmétique de premier terme u₀ = -3 et de raison 3,5. Quelle est l'équation de la droite sur laquelle ils sont alignés ?
Introduction aux suites numériques : Suites géométriques
Introduction aux suites numériques/Suites géométriques
Une page de Wikiversité.
| Chapitre 3 | |||
| Leçon : Introduction aux suites numériques | |||
|---|---|---|---|
| Chap. préc. : | Suites arithmétiques | ||
| Chap. suiv. : | Comportement asymptotique | ||
Sommaire[masquer] |
[modifier] Définition par récurrence
|
Définition |
|
Une suite est géométrique quand on multiplie toujours par le même nombre pour passer d'un terme au suivant. Une suite géométrique est donc définie par :
Le facteur q qui permet de passer d'un terme au suivant s'appelle la raison de la suite (un). |
[modifier] Être ou ne pas être une suite géométrique
Parmi les suites ci-dessous, lesquelles sont géométriques ? Dans ce cas, donner leur raison.

- 3, 9, 27, 81, ...
- 1, -5, 25, -125, 625, ...
- 10; 5; 2,5; 1,25; 0,625; ...
- 2, 4, 9, 16, 25, 36, 49, 64, 81, 100, ...
[modifier] Terme général d'une suite géométrique
Pour arriver à un, il faut multiplier n fois par la raison q le premier terme u0
|
Théorème |
|
Le terme général d'une suite géométrique  |
[modifier] Utilisation du terme général
- Soit (un) une suite géométrique telle que u0 = 3 et q = 1,5. Calculer u11
- Soit (un) une suite géométrique telle que u0 = 0,5 et q = -2. Calculer u25
- Soit (un) une suite géométrique telle que u1 = 8 et q = 0,25. Calculer u10
- Soit (un) une suite géométrique telle que u15 = 320 et q = 3. Calculer u0
- Soit (un) une suite géométrique telle que u11 = 25 et u14 = 200. Calculer u0 et q.
[modifier] Sens de variation
|
Théorème |
|
Une suite géométrique de premier terme positif et de raison q est :
|
[modifier] Somme des termes d'une suite géométrique
|
Théorème |
|
La somme des n+1 premiers termes d'une suite géométrique est donnée par la formule :  |
[modifier] Calculs de sommes
En utilisant la formule,
1. Soit (un) une suite géométrique telle que u0 = 3 et q = 2. Calculer 
2. Calculer 
[modifier] Exercice
Exercice : Exercices sur les suites arithmétiques
Introduction aux suites numériques/Exercice/Suites arithmétiques
Une page de Wikiversité.
| Exercice 2 | |||
| Leçon : Introduction aux suites numériques | |||
|---|---|---|---|
| Chapitre du cours : | Suites géométriques | ||
|
Cet exercice est de niveau 11. |
|||
Sommaire[masquer] |
[modifier] Exercice 1
1. Soit (Un) une suite arithmétique de raison 3,5 et de premier terme U0 = 2.
- a. Calculer (U24).
- b. Calculer S24 = U0 + U2 + ... + U24
2. Soit (Vn) une suite arithmétique.
On donne V10 = 39 et V30 = 84.
Calculer le premier terme V0 et la raison de cette suite.
[modifier] Exercice 2
1. Soit (Un) une suite arithmétique de raison 2,5 et de premier terme U0 = 2.
- a. Calculer (U14).
- b. Calculer U1 + U2 + ... + U14
2. Soit (Vn) une suite arithmétique.
On donne V5 = 39 et V14 = 84.
Calculer le premier terme V0 et la raison de cette suite.
[modifier] Réseau
Le nombre d'abonnés d'un réseau téléphonique passe de 15 à 18 millions en un an. On suppose qu'ensuite il augmente chaque année régulièrement du même nombre : 3 millions par an.
Si on note U0 = 15 000 000 le nombre d'abonnés initial, et Un le nombre d'abonnés après n années, on a U1 = 18 000 000.
- 1. Calculer U10
- 2. Exprimer Un en fonction de n.
[modifier] Chiffre d'affaire
Le chiffre d'affaires du rayon « petit outillage » d'un magasin s'accroît tous les ans de 50 000 F.
En 1997, le chiffre d'affaires C0 était de 500 000 F. On note Cn le chiffre d'affaires au cours de l'année (1997 + n).
- 1. Expliquer pourquoi (Cn) est une suite arithmétique et donner sa raison r.
- 2. a. Exprimer Cn en fonction de n.
- b. Calculer le chiffre d'affaire en 2005.
- c. En quelle année peut-on prévoir un chiffre d'affaires de 1 050 000 F ?
[modifier] Chute libre
Un corps tombant en chute libre parcourt 4,9 m pendant la première seconde ; 14,7 m pendant la deuxième seconde ; 24,5 m pendant la troisième seconde et ainsi de suite. Ces distances sont les termes consécutifs d’une suite arithmétique.
- 1. Déterminer la distance parcourue pendant la dixième seconde.
- 2. Déterminer la distance parcourue en 10 secondes.
Exercice : Exercices sur les suites géométriques
Introduction aux suites numériques/Exercice/Suites géométriques
Une page de Wikiversité.
| Exercice 2 | |||
| Leçon : Introduction aux suites numériques | |||
|---|---|---|---|
| Chapitre du cours : | Suites géométriques | ||
|
Cet exercice est de niveau 11. |
|||
Sommaire[masquer] |
[modifier] Exercice 1
1. Soit (Un) une suite géométrique de raison 1,5 et de premier terme U0 = 2.
- a. Calculer (U9).
- b. Calculer S9 = U1 + U2 + ... + U9
2. Soit (Vn) une suite géométrique.
On donne V7 = 15309 et V9 = 137781.
Calculer le premier terme V0 et la raison q de cette suite.
[modifier] Exercice 2
1. Soit (Un) une suite géométrique de raison 1,5 et de premier terme U0 = 2.
- a. Calculer (U7).
- b. Calculer S7 = U1 + U2 + ... + U7
2. Soit (Vn) une suite géométrique.
On donne V9 = 15309 et V11 = 137781.
Calculer le premier terme V0 et la raison q de cette suite, sachant que la raison est positive.
[modifier] Bactéries
On note U0 = 100 000 une population initiale de bactéries.
On remarque que tous les jours cette population est multipliée par 1,7.
1. Si Un désigne la population après n jours, quelle est la nature de la suite (Un) ? Justifier.
2. Calculer le nombre de bactéries après 10 jours.
3. En supposant que chaque jour, une bactérie donnée peut soit mourir, soit se diviser en deux.
Calculer le pourcentage de bactéries qui meurent à chaque étape.
[modifier] Du blé sur l'échiquier
On pose un grain de blé sur la première case d'un échiquier, deux sur la deuxième, quatre sur la troisième, etc. Combien de grain de blé faut-il pour remplir les 64 cases ?
[modifier] C'est tout bénéfice
Le bénéfice d'un entrepreneur augmente de 0.5% par mois pendant 10 ans.
La première année, il était de 200000 €.
Quel est son bénéfice total sur 10 ans ?


 )
)



 donc
donc  . De plus,
. De plus,  .
.



 .
.






 est une suite arithmétique, de raison r = 3 000 000. D'après le cours, on sait alors que pour tout n :
est une suite arithmétique, de raison r = 3 000 000. D'après le cours, on sait alors que pour tout n : avec r= 50000
avec r= 50000







